Die Widersprüche in der gängigen Behandlung der spontanen Emission eines Photons.

Download PDF

Eine ergänzende Zusammenfassung zu den Artikeln

Emission eines Photons - ohne Quantensprung!
Emission zweier Photonen - ohne Quantensprung!
Eine kleine Galerie zu atomaren Dipol-Übergängen
Spontaneous photon emission revisited

Die Abbildung aus S. Kikuchi, Zeitschrift für Physik, July 1930, Volume 66, Issue 7–8, pp 558–571,
„Über die Fortpflanzung von Lichtwellen in der Heisenberg-Paulischen Formulierung der Quantenelektrodynamik“ zeigt den zeitlichen Verlauf des Erwartungswertes der Energiedichte (Quadrat der elektrischen Feldstärke) des elektrischen Feldes nach der Aussendung eines Lichtquants durch ein Atom (im Ursprung) in der Entfernung R.
Der Artikel basiert auf der Weisskopf-Wigner-Näherung (im Folgenden WWN),
V. Weisskopf und E. Wigner, ZS. f. Phys. 63, 54, 1930, „Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie“, die bis heute als Standard für die Behandlung der spontanen Emission eines Photons gilt. Die Grundannahmen der WWN sind:

1. Die Emission beginnt zu einem bestimmten Zeitpunkt (z.B. t = 0) mit maximaler Amplitude.

2. Das angeregte Niveau „zerfällt“ exponentiell, in Analogie zum radioaktiven Zerfall oder zum gedämpften harmonischen Oszillator.

Sowohl diese Annahmen, als auch die mathematische Behandlung und insbesondere die physikalische Interpretation beinhalten eine Reihe von Widersprüchen.

Zu 1.:

• Eine sprunghafte Änderung der Feldstärke und Energie führt nicht nur in der klassischen Physik (Maxwell) zu Divergenzen. So müsste z.B. für t = 0 die magnetische Feldstärke unendlich werden.

• Obwohl der Artikel von Kikuchi zeigen soll, dass sich das elektrische Feld (insbes. der Sprung in der Feldstärke) nicht schneller als mit Lichtgeschwindigkeit ausbreitet, verletzt schon der Sprung selbst das Kausalprinzip (siehe z.B.  Jackson, Classical Electrodynamics, Wiley 1962, S. 599).
  

• In der Quantenphysik kann man einen Zeitpunkt prinzipiell nicht exakt bestimmen, bzw. eine beliebig schnelle Zustandsänderung wäre mit einer beliebig großen Energieunschärfe verbunden.

Zu 2.: In der WWN geht man von folgendem Zustand aus

Die WWN setzt ein exponentielles Abklingen von a(t) explizit voraus, tatsächlich ergibt sich das aber auch ohne diese spezielle Annahme aus der Linearität der Schrödingergleichung (SGL), zusammen mit den anderen „üblichen Annahmen“ (WWN und Folgeartikel) die dazu dienen, eine geschlossene Lösung zu ermöglichen. Als Analogie (oder gar als Begründung?) wird der gedämpfte harmonische Oszillator (mechanisch oder elektrisch) der klassischen Physik angeführt - was ja auch gut zum exponentiellen Zerfall radioaktiver Kerne (also auch quantenmechanisch?) passt. Dabei übersieht man:

• Ein einzelnes Atom (geschweige denn ein Ensemble) kann nicht so präpariert werden wie eine gespannte Feder oder ein Kondensator (in einem Schwingkreis). Und auch beim Schließen eines klassischen Schalters beginnt der Strom erst nach einer endlichen Zeit merklich zu fließen, springt also nicht in unendlich kurzer Zeit von 0 auf einen endlichen Wert.

• Selbst wenn o.g. Präparation möglich wäre, befände sich das Atom (das Ensemble) in einem stationären Zustand (lt. Voraussetzung der WWN) mit a(t)=1 und alle b_k(t)=0, besitzt also kein Dipolmoment und kann nicht strahlen. Also muss man eine Anleihe beim Vakuum machen, das früher oder später (exponentiell abklingend natürlich) das Atom aus seinem stationären Zustand kippt. Das mag ja der Fall sein, aber:

• Kurz nach t = 0 hat das Atom ein verschwindend kleines Dipolmoment, kann also nicht strahlen wie ein Hertzscher Dipol, den man erst voll auflädt und dann zur Zeit t = 0 anschaltet (Funkeninduktor).

• Die (lineare) Überlagerung zweier QM-Zustände (obiger Ansatz) führt zu einer Schwebung mit einer Übergangsfrequenz (Differenzfrequenz), während ein klassischer Oszillator mit seiner Eigenfrequenz schwingt (mit Verschiebung durch Dämpfung), die man also der Eigenfrequenz des angeregten Zustands gleichsetzen müsste. Eine bessere Analogie wären also gekoppelte Pendel oder Schwingkreise.

• In obigem Ansatz wird der EES ignoriert: Man summiert zwar über verschiedene Moden k, also die Energien des Photons, aber nicht über verschiedene Energien des angeregten Zustands |a> (bei natürlich fester Energie des Grundzustand |g>). Dieser Fehler wird dann nachträglich in eine Energieunschärfe des angeregten Zustands „zurückgerechnet“. Das mag ja praktikabel sein, aber dann war der unscharfe angeregte Zustand wohl nicht exakt stationär? Fand vielleicht deshalb die Emission spontan statt - ganz ohne Vakuum?
  

Eine entscheidende Rolle in allen „Theorien“ (oder besser Näherungen), die Übergänge mit Sprüngen erklären, spielen die „stationären Zustände“ und ihre Fehlinterpretation:

• Stationäre Zustände: Diese Altlast der Fehlinterpretation hat tiefe Wurzeln (Bohr, Heisenberg), die noch heute schöne Blüten treiben. Stationäre Zustände werden weiterhin gerne mit stabilen Zuständen verwechselt: die Bohr-Heisenbergsche Echokammer (BHCQED :-) hat einen langen Nachhall! Aber schon Schrödinger wusste, dass es sich dabei nur um zeitunabhängige Zustände handelt - zeitunabhängig im Sinne der mathematischen Beschreibung und nicht im Sinne eines stabilen Gleichgewichts.

  • In der Realität kommen stationäre Zustände nicht vor! Egal ob man versucht, einen Bleistift so auf die Spitze zu stellen, dass er nicht umfällt, oder ein Atom (oder gar ein Ensemble von Atomen) so zu präparieren, dass der stationäre Zustand zu einem stabilen Zustand wird, es würde unendlich lange dauern.
    

  • Der „normale Zustand“ eines Atoms (des „strahlenden Elektrons“) ist also der kontinuierliche Übergang von einem „Anfangszustand“ höchster Energie (woher auch immer) in den Grundzustand (tiefster Energie, inklusive Einfang durch den Kern). In der Regel (Dipolübergang) leben „stationäre Zustände“ nur 10^-8s. Also das genaue Gegenteil des Bohrschen Atommodells!
    

  • Solange sich das Elektron im Kontinuum „bewegt“ (z.B. mit einem Bahnimpuls), stehen ihm „stationäre Zustände“ im Kontinuum zur Verfügung: z.B. Bremsstrahlung bis zur kw. Grenze. Danach (unterhalb der „vollständigen Abbremsung“) gibt es die stationären Zustände nur noch mit einem diskreten Spektrum. Natürlich muss sich das Elektron immer an gewisse „Auswahlregeln“ halten (mehr oder weniger: EES, IES…), aber bitte nicht an Bohrs Verbote!
    

  • Unterhalb der kurzwelligen Grenze, bzw. der Ionisationsgrenze: Rydbergzustände, langsames „Herunterspiralen“.
    

  • Überlagerung von mehr als zwei Zuständen mit „kontinuierlichen Gewichten“ siehe z.B. "Das gefangene Wellenpaket". Das Zweiniveau-System ist nur eine primitive Näherung!
    

  • Und dann gibt es noch die Zustände mit kontinuierlicher Energie, aber mit Quantenzahlen l, m.
    

  • Und nicht zu vergessen die Streuwellen und Bremsstrahlung. Der Anfangszustand ist immer "stationär", aber sicher nicht stabil!
    
    

Mit anderen Worten: Ein stationärer Zustand ist nichts weiter als ein Zustand, der sich durch psi(r,t) = u(r)*exp(i*omega*t) mathematisch beschreiben lässt, sodass die Zeitabhängigkeit beim Bilden des Betragsquadrats „für alle Zeiten“ verschwindet. Physikalisch bedeutet das aber nicht, dass der Zustand „für alle Zeiten“ bestehen bleibt, also stabil ist, sondern sich auch „spontan“ (also ohne äußere Einwirkung) ändern kann, z.B. durch Kopplung an das QED-Vakuum.

• Dipolmoment: Stationäre Zustände haben kein Dipolmoment (oder Multipolmoment), können also nicht strahlen. Die Ladungsverteilung schwingt zwar formal/mathematisch wie eine „stehende Welle“ (Saite / Membran), aber mit einer komplexen Amplitude, es fließt kein Strom (siehe Elektrofluid). Und wie oben erwähnt ist die Frequenz der Strahlung nicht die Frequenz des angeregten Zustands, sondern die Differenzfrequenz zweier Zustände. Erst die Überlagerung von Zuständen besitzt ein Dipolmoment (Interferenzterm). Und zwar nicht nur ein statisches mittleres (räumlich), sondern ein zeitlich veränderliches.
  

• Linienform: Der Schluss vom „exponentiellen Zerfall“ auf ein Spektrum einer Schwingung ist bedenklich. Zerfälle sind zufällige inkohärente Vorgänge. Nicht alles, was exponentiell abklingt, ist eine Schwingung mit einer exponentiell abklingenden Amplitude. Welche Linienform kann man einem α-Zerfall zuordnen, oder der Entladung eines Kondensators, oder dem Würfeln?
  

• "Photonenform": Die „Ortsfunktion eines Photons“ ist in der QM/QED nicht streng definiert (weil das Photon keine Ruhemasse hat - verkürzt gesagt). Pragmatiker arbeiten mit Gaußpaketen, was z.B. durch die Form des "HOM-Dips" bestätigt wird, aber auch durch neure Messungen der "Amplituden von Biphotonen".
  

• Kaskaden: Wenn die Übergänge eines Atoms wie radioaktive Zerfälle ablaufen würden ("dem radioaktiven Zerfallsgesetz folgen würden"), dann müssten Kaskadenübergänge "simultan" ablaufen (was zwar möglich ist, aber von Weisskopf-Wigner selbst ausgeschlossen wird).
  
  

Zitate und Standard-QED:

Die Liste der Zitate, in denen man versucht, den Akt (Sprung) der spontanen Emission und den Prozess der Ausstrahlung unter einen Hut zu bringen, wäre beliebig lang. Stellvertretend seien hier zwei Quellen genannt, die sich auf die WWN beziehen:

W. Heitler, The Quantum Theory of Radiation, 3. Ausgabe, S. 184: "The intensity distribution of the emitted line is given by the probability function of the final state b_a1λ. After the time t>>1/γ, when the atom certainly jumped down, the probability that a quantum h*ν has been emitted is given by [Lorentzlinie]..."

M.O. Scully, M.S. Zubairy, Quantum Optics, 6. Auflage, S. 208: "During the process of spontaneous emission, the atom emits a quantum of energy equal to E_a - E_b = h*ν. We now calculate the state of the field emitted during the spontaneous emission process. Auf S. 209 findet man dann "...can be interpreted as a kind of wave function for a photon".

So mogelt man sich elegant um den Dualismus herum, den man selbst eingeführt hat: Das Elektron muss von einem stationären Zustand zu einem anderen stationären Zustand springen, aber dabei muss "eine Art Welle" herauskommen. Die Amplitude dieser Welle muss exponentiell abklingen, weil ein Ensemble von Atomen exponentiell zerfällt, und deshalb ist das Spektrum "des Photons" eine Lorentzlinie! Alles klar?

Weshalb ist die QED dennoch so erfolgreich?
Weil sie mittelt und auf die Beschreibung der Dynamik der Elementarprozesse verzichtet.
Natürlich kann man Verschränkung nicht klassisch beschreiben. Aber umgekehrt ist die lineare QED bis heute nicht in der Lage, hoch auflösende Experimente zu beschreiben: für den zeitlichen (kontinuierlichen) Ablauf werden immer klassische - wellenmechanische, Schrödingersche - Modelle verwendet. Und nichtlineare! Aber natürlich kann man auch nichtlineare Prozesse quantisieren.
Umgekehrt: Den bisherigen Beschreibungen der Dynamik fehlt die richtige Art der Mittelung, um den Emissionsprozess (Dämpfung und Linienverschiebung) „korrekt“ zu beschreiben (wobei „korrekt“ die experimentelle Beobachtbarkeit beinhaltet)! Das fängt schon damit an, dass man das Elektron als punktförmige Ladung behandelt und nicht als Ladungsverteilung (Stichwort: Lorentzmodell).


Wie kann man die Widersprüche der WWN vermeiden?

Erster Versuch: Der Sprung zur Zeit „t=0“ lässt sich vermeiden, wenn man die Superposition (und damit das Dipolmoment) zeitabhängig formuliert, siehe
Emission eines Photons - ohne Quantensprung!

Die Fouriertransformierte dieser Schwingung (des Photons) ist nun (im Vergleich zur Näherung von Weisskopf und Wigner) aber keine Lorentzlinie, sondern eine "Beta-Linie":

                  

mit der Eulerschen Betafunktion B(x,y) zur zentralen Frequenz w0 (imaginäre Einheit als I notiert, w als Frequenz).

Das ist natürlich "rein phänomenologisch", aber auch nicht phänomenologischer als die WWN.

Mit der „Beta-Linie“ bleibt die Kaskade unbefriedigend, siehe Emission zweier Photonen - ohne Quantensprung!, weil das "exponentielle Zerfallsgesetz"

weiterhin vorausgesetzt wird. Es lassen sich aber eine ganze Reihe von kontinuierlichen Übergängen visualisieren: Eine kleine Galerie zu atomaren Dipol-Übergängen

Zweiter Versuch:
Spontaneous photon emission revisited

Stellt man die Zeitabhängigkeit des Dipolmoments in den Vordergrund und gibt nicht ein "exponentielles Abklingen" als Lösung vor, so erhält man mit der Proportionalitätskonstanten k die Differentialgleichung für die Besetzungszahl des "Grundzustands": 

auch bekannt als die logistische Differentialgleichung. Sie hat die "standartisierte" Lösung ((0)=1/2): 

 =  

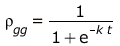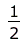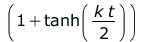
auch bekannt als logistische Funktion, oder kumulative logistische Verteilung. 

Das Frequenzspektrum erhält man durch Fouriertransformation. Die Amplitude der E-Feldstärke ist proportional zur Wurzel der Energie (od. Leistung): 

Auch bekannt als hyperbolic secant distribution. 

Die Fouriertransformierte von E(t) ist dann 

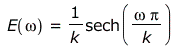
und ihr auf 1 normiertes Quadrat, also das Intensitätsspektrum für ein Photon mit der Energie 1 

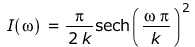
Diese Phänomenologie passt zwar nicht zur linearen Schrödingergleichung, aber es gibt ja auch die nichtlineare Schrödingergleichung. Dazu kommt: Photonen mit sech-Profil sind bei Atomen besonders beliebt: Superradianz!

© August 2018, Dr. Michael Komma (VGWORT)

Ergänzung im Juli 2019: Eine weitere Recherche zu und in den Minev/Carmichael/Devoret-Artikeln ergab, dass die logistische Gleichung auch in der Quantenphysik schon länger bekannt ist, aber nicht als solche benannt (erkannt?) wird. Dabei kommt es nicht auf den Namen der Gleichung an, sondern auf ein fundamentales Problem der QM/QED: die Dynamik eines Übergangs lässt sich mit der linearen SGL, bzw. linearen "Bewegungsgleichungen" nicht beschreiben, also werden nichtlineare Vorgänge ausgeblendet. Leider wurde mit diesem "linearen Ansatz" auch die "Neoklassische Theorie" (NCT) von E.T. Jaynes über Jahrzehnte ausgeblendet, zumal er ja seine Wette verloren hatte.
Hier ist ein Einstiegspunkt in die NCT: https://bayes.wustl.edu/etj/articles/survey.nct.pdf

In dem Anfang Juni 2019 veröffentlichten Artikel To catch and reverse a quantum jump mid-flight, wird experimentell nachgewiesen, dass ein atomarer Übergang kontinuierlich und deterministisch abläuft (zumindest in einem künstlichen Atom). Die theoretische Behandlung erfolgt mit "Quantentrajektorien" und führt im Endeffekt auf das gleiche Ergebnis wie im Logistischen Modell vorgeschlagen.

Siehe auch: Galerie | Kaskade | Spontane Emission, logistisch | Weisskopf-Wigner | Ensemble-Individuum | Superradianz | Atomarer Dipol 

Weitere Links: Matrixoptik | Doppelspalt und Dualismus | Quantenradierer | Photon am Doppelspalt | Gitter | Punktgitter | Kreuzgitter | Raumgitter | Beugung | Fresnelbeugung | Zeiger | Interferenz

Moderne Physik mit Maple

komma_AT_oe.uni-tuebingen.de

HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top