Hertz

Elektrizität

Download PDF-Zusammenfassung Elektrizität

Kurze Übersicht mit Links zu Themen der Elektrodynamik auf mikomma.de

Hertzscher Dipol

mikomma.de

Wie breiten sich die elektromagnetischen Wellen von einem Hertzschen Dipol aus? Und wie kann man es erklären, dass die magnetische Feldstärke und die elektrische Feldstärke direkt am Dipol um 90° phasenverschoben sind, während sie in der Fernzone in Phase sind? (Manchmal spricht man scherzhaft auch davon, dass das B-Feld das E-Feld einholt - oder war es umgekehrt?)

Vielleicht kann man diese Fragen mit Maple beantworten.

Die magnetische Feldstärke lautet:

[Maple Math]

Siehe z.B. Jackson, Classical Electrodynamics. Die x-, y-, z-Komponenten sind durch Kommata getrennt, die imaginäre Einheit ist als großes I notiert. Der Vektor n ist der Einheitsvektor in Richtung der Ausstrahlung ("Radiusvektor") und der Vektor p hat die Richtung des Dipolmoments.

Die elektrische Feldstärke lautet:

[Maple Math]

Die Feldstärken enthalten Summanden, die mit 1/r, 1/r² und 1/r³ gehen. In der Fernzone bleiben nur die 'Strahlungskomponenten' mit 1/r übrig: E und B sind in Phase. In der Nahzone (genauer für r -> 0) ist B gegenüber E um I (also 90°) phasenverschoben.

Wir machen einen ersten Versuch (E-Feld rot, B-Feld blau, wegen der Divergenz der Feldstärken bei r = 0, beginnt die r-Achse in den folgenden Darstellungen nicht bei Null):

[Copyright M. Komma]

Offensichtlich wurde für die Zeichnung die Wellenlänge 2 gewählt. Die Nullstellen von E und B fallen praktisch zusammen (die Vorzeichen von E und B wurden so gewählt, dass die Kurven deutlich getrennt sind). Sind wir bei r = 2 schon in der Fernzone? Gibt es überhaupt eine Phasenunterschied von E und B? Wir sollten die Nahzone untersuchen:

[Copyright M. Komma]

In dieser Animation sieht man, weshalb man von der 'Nahzone' spricht: Der Phasenunterschied von E und B macht sich nur unterhalb der halben Wellenlänge bemerkbar (Vorzeichen von E und B so gewählt, dass die Kurven in der Fernzone zusammenfallen).

Nun sind die Feldstärken ja auch räumlich unterschiedlich orientiert. Kann man das mit Maple darstellen?

So sieht also die Geburt einer elektromagnetischen Welle aus! Es ist wunderbar, der Natur beim Stricken zuzusehen! Aber die Natur strickt keine linearen elektromagnetischen Wellen - sie kann es dreidimensional (mindestens). Mit Maple können wir noch eine Dimension weiter mithalten:

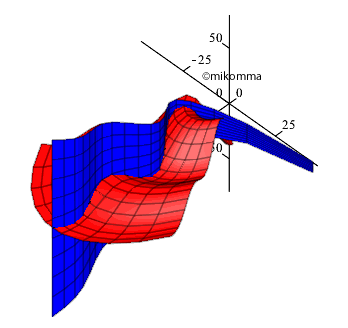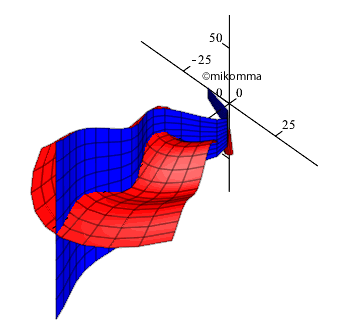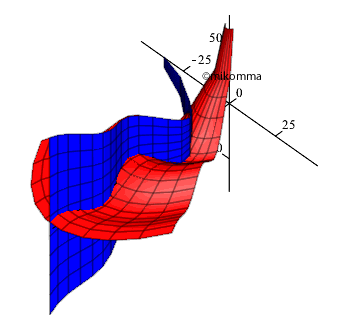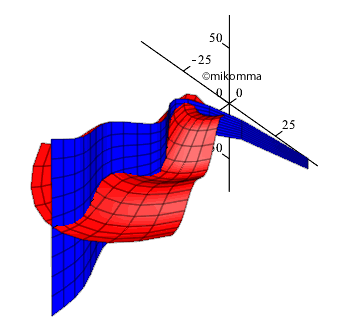
Download Movie: avi-Datei, QuickTime Player

Mit unserem Verstand und unserem Vorstellungsvermögen kommen wir noch eine Dimension weiter:

Noch ein paar statische Bilder...

Das magnetische Feld ist rotationssymmetrisch um die Dipolachse. Wie könnte es auch anders sein? Leider wird es in so manchen Lehrbüchern bis zum heutigen Tag nicht so dargestellt, sondern man findet immer wieder die falsche 'Verkettung' von E und B. In der nebenstehenden Abbildung wurden die Pfeile der Feldstärke proportional zum Abstand von der Dipolachse skaliert, um eine bessere Wiedergabe zu erreichen. Natürlich lässt sich im originalen Maple-Worksheet die 3D-Darstellung interaktiv manipulieren.
Das elektrische Feld des Hertzschen Dipols hat keine azimutale Komponente und steht somit immer senkrecht zum B-Feld. In der nebenstehenden Abbildung sind die Pfeile wieder mit dem Abstand skaliert: statt E, E*r. Natürlich lässt sich im originalen Maple-Worksheet die 3D-Darstellung interaktiv manipulieren.
Sowohl die magnetische als auch die elektrische Feldstärke (ihr Betrag) haben die nebenstehend abgebildete räumliche Struktur in der 'Fernzone'.	von vorne	leicht schräg
Und mit etwas Phantasie setzen wir das nun alles zusammen. Natürlich lässt sich im originalen Maple-Worksheet die 3D-Darstellung interaktiv manipulieren.
Aber vielleicht sollten wir doch noch den Klassiker mit einer besseren Auflösung laufen lassen: Feldlinien des elektrischen Feldes. So lösen sich also die E-Wirbel ab! Was bedeutet wohl die Einfärbung der Feldlinien? Mehr Details zur "Abnabelung" der E-Wirbel sind hier zu sehen: Ergänzungen.
Wenn man in der obigen Darstellung in Gedanken (oder mit einem Blatt Papier auf dem Bildschirm) Tangenten vom Ursprung an die geschlossenen E-Wirbel legt (es gibt sechs Möglichkeiten), erkennt man, dass das E-Feld auch in (oder gegen) die Ausbreitungsrichtung der Welle zeigen kann: Die E-Welle ist nur auf der Mittelsenkrechten (Mittelebene) rein transversal. In der Darstellung des E-Feldes als Vektorfeld, findet man deshalb auch in der Fernzone Stellen, an denen die Pfeile rotieren (und nicht nur ihre Länge ändern). (Bei der Fixierung einer Stelle ist der Mauszeiger hilfreich.)
Aber bitte mit B-Feld! Also: Im Strahlungsfeld eines Hertzschen Dipols sind die B-Linien immer rotationssymmetrisch um die Dipolachse und bilden keine "Kette" mit den E-Wirbeln wie bei Gaußstrahlen.

komma(AT)oe.uni-tuebingen.de