Licht im Medium

© 2007, frei nach R.P. Feynman, The Origin of the Refractive Index  

"Warum bewegt sich Licht im Medium langsamer als im Vakuum?"

Man liest bisweilen die Erklärung, dass die Photonen in den Atomen des Mediums kurz anhalten ("Absorption und Reemission") und so das Licht gebremst wird, also seine Phasengeschwindigkeit kleiner wird. Manche Wiki-Physiker berufen sich mit dieser Erklärung auf die Feynman-Lectures (Vol. I, 31),  obwohl dort das genaue Gegenteil steht:

Feynman verwendet das klassische Modell. Das Medium besteht aus (gedämpften) Oszillatoren, die von der primären Lichtwelle zu Schwingungen angeregt werden. Außerhalb der Resonanzfrequenz der Oszillatoren (Atome mit Dipolmoment) findet keine Absorption statt und die Oszillatoren werden zu einer Schwingung gezwungen, die unterhalb ihrer Resonanzfrequenz in Phase mit der primären Lichtwelle ist, wobei sich die primäre Lichtwelle auch im Medium mit Vakuumlichtgeschwindigkeit bewegt. Soweit nichts Neues, das ist die klassische Berechnung des Brechungsindex. Aber nun kommt Feynmans "Trick":

Frei nach Huygens (oder Feynmans Pfadintegralen?) muss die (komplexe) Amplitude der Welle in jedem Raumpunkt die Summe der Amplituden aller Elementarwellen, die diesen Punkt erreichen, sein. Also berechnet Feynman die Amplitude der elektrischen Feldstärke, die von einer dünnen (ebenen) Schicht von Oszillatoren in einem Punkt hinter dieser Schicht erzeugt wird (Vol. I, 30-7). Und - man staune! - die von einer Schicht resultierende gestreute Welle hinkt der Primärwelle um 90° hinterher. Es handelt sich also nicht um die Phasenverschiebung, die bei der Anregung eines Oszillators in Resonanz entsteht, und somit nicht um Absorption. Addiert man die Amplitude der gestreuten Welle zur Amplitude der Primärwelle, so ergibt sich für die hinter der dünnen Schicht resultierende Welle die erwartete Verzögerung.

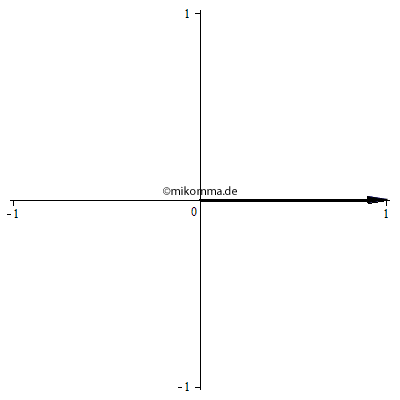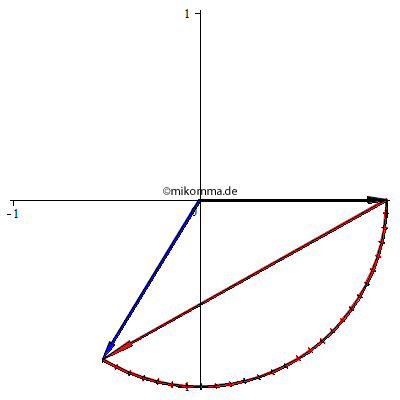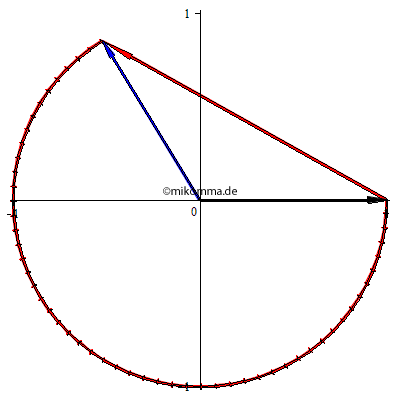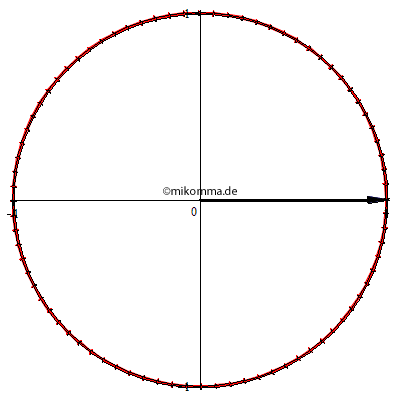
Feynmans Phasenschieber Stellt man die komplexe Amplitude der primären Welle als schwarzen Pfeil (in der komplexen Ebene) dar, so wird ihre Phase nach jeder dünnen Schicht verzögert (kleine rote Pfeile). Das Ergebnis ist der blaue Pfeil - im Folgenden "die resultierende Welle". (Siehe Feynman Lectures Vol. I, Fig. 31-3.) Für das Weitere noch eine Anmerkung: "Streuung" heißt in diesem Zusammenhang immer kohärente Streuung, genauer gesagt kohärente Vorwärtsstreuung. Der rote Pfeil, der vom schwarzen Pfeil zum blauen Pfeil zeigt, ist also die Summe aller (komplexer) Amplituden der Sekundärwellen mit fester Phasenbeziehung zur Primärwelle.

Also wie funktioniert das nun? Es gibt zwei Arten der Modellierung:

1. Iteration: Die Phasenverschiebung der gestreuten Wellen wird multiplikativ (Faktor exp(i*phi)) berücksichtigt, also eine UND-Verknüpfung der Pfade.

2. Huygens pur: Alle Elementarwellen werden aufsummiert, also eine ODER-Verknüpfung der Pfade.

1. Iteration

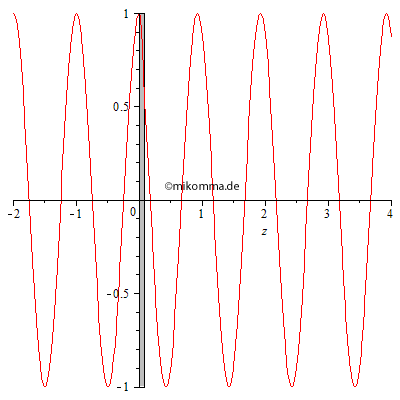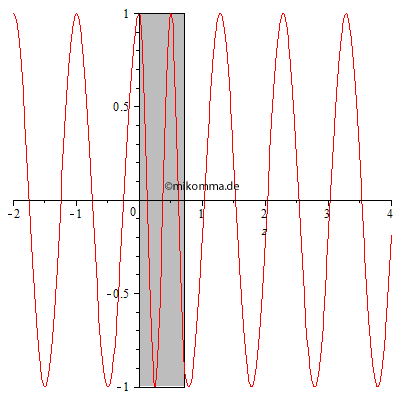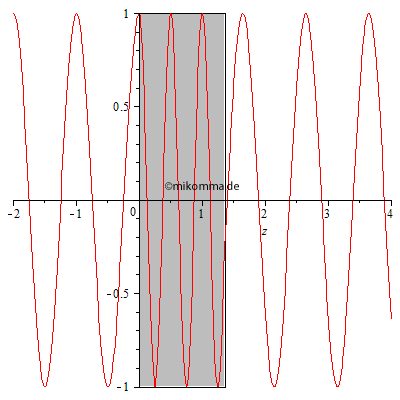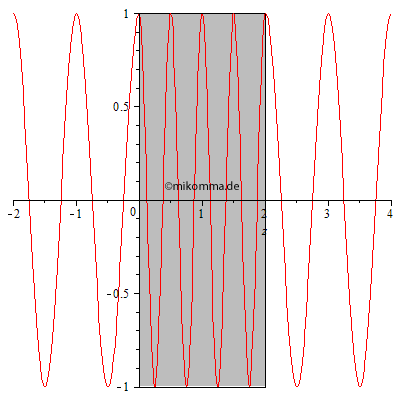
Feynmans Näherung gilt für eine dünne Schicht. Aber man kann natürlich das Verfahren wiederholen und mehrere dünne Schichten hinter einander setzen. Die nebenstehende Animation zeigt das Ergebnis, wenn man in der Berechnung die Zeit festhält und die Dicke des Mediums (grau) anwachsen lässt: Hinter dem Medium (rechts) läuft die Welle nicht rückwärts, sondern wird immer stärker verzögert. Das gilt natürlich auch im Medium, wo deshalb die Wellenlänge kürzer ist. Die kürzere Wellenlänge im Medium ist aber nicht auf eine kleinere Phasengeschwindigkeit zurückzuführen, sondern auf eine Phasenverschiebung durch die gestreute Welle. Die Phasengeschwindigkeit einer elektromagnetischen Welle, die von einer einzelnen oszillierenden Ladung ausgeht, hat überall den Wert der Lichtgeschwindigkeit im Vakuum. Erst durch die Überlagerung mit anderen Wellen kann es zu einer scheinbaren Verlangsamung der Phasengeschwindigkeit kommen. Aber es ist natürlich zweckmäßig, mit dieser scheinbaren Phasengeschwindigkeit (verkürzte Wellenlänge durch unveränderte Frequenz) zu rechnen.

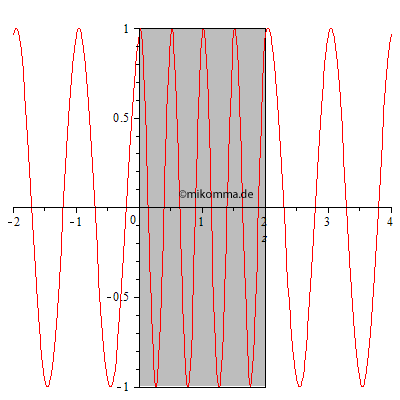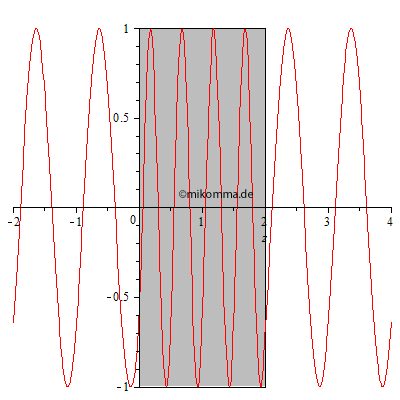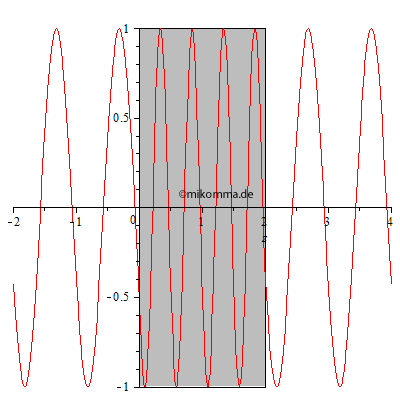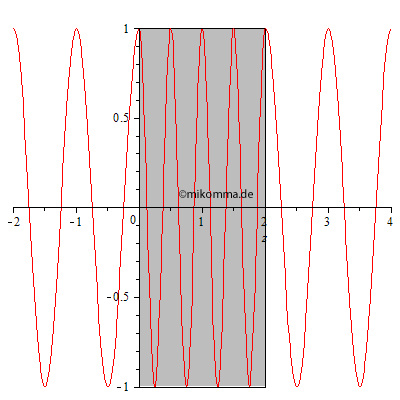
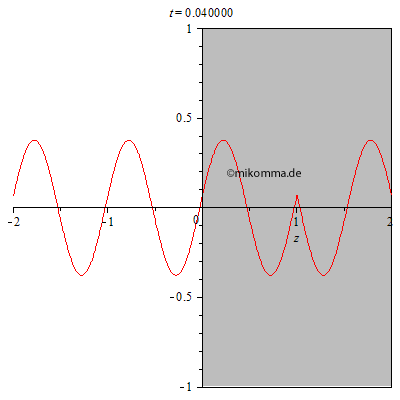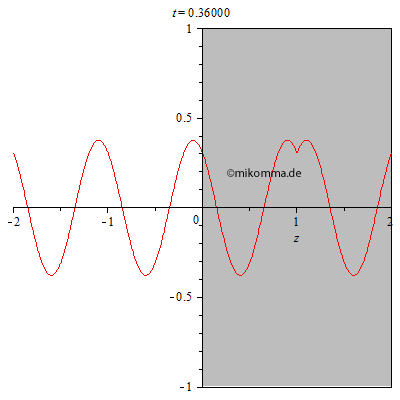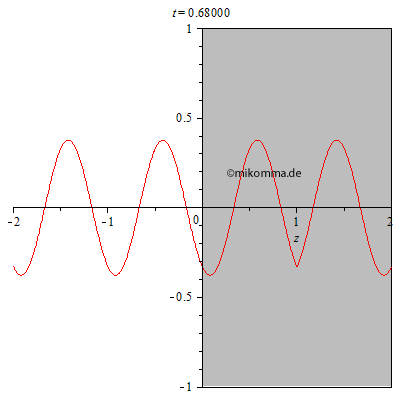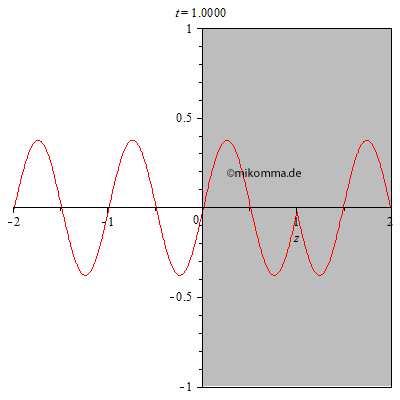
Das Experiment, in dem die Dicke des Mediums zu einem festen Zeitpunkt variiert wird, muss erst noch erfunden werden. Wir berechnen also nach obiger Methode den Durchgang einer Lichtwelle durch ein Medium: In der nebenstehenden Animation wurden 100 dünne Schichten mit dem Brechungsindex 2 zu einem Medium (grau) mit der Dicke 2 zusammengesetzt. Die resultierende Welle wurde von Schicht zu Schicht iterativ berechnet.

Beim ersten Lesen denkt man bei Feynmans Ausführungen an Hokuspokus, weil in die Berechnung das hineingesteckt wird, was herauskommen soll: Eine Phasenverschiebung der Welle hinter dem Medium, die zunächst als Produkt zweier komplexer Zahlen dargestellt wird (wie in den obigen Darstellungen). Aber Feynman geht der Sache auf den Grund. Die Physik muss in der Überlagerung von Wellen, also der Summe komplexer Zahlen zu finden sein - frei nach Huygens. Die folgenden Animationen sind nach diesem Prinzip berechnet (im Gegensatz zu Feynmans Lectures nicht in Näherung erster Ordnung, sondern exakt).

Man wird sehen: Der iterative Ansatz ist eher phänomenologisch. Die echte Physik steckt in Huygens' Prinzip.

2. Huygens

Eine ebene Welle (im Bild nicht dargestellt) trifft in z-Richtung auf ein Medium und erzeugt dort an den "Streuzentren" sekundäre Elementarwellen (rot). Alle Elementarwellen bewegen sich mit Vakuumlichtgeschwindigkeit - auch im Medium. Nur ihre Phase hängt vom Medium ab. Rechts ist eine solche Elementarwelle dargestellt (mit überhöhter Amplitude), die ihr Zentrum in der Mitte des Mediums hat und sich von dort in positive und negative z-Richtung ausbreitet. (Natürlich gehen von Elementarzentren Kugelwellen aus, aber die Darstellung einer 'eindimensionalen Welle' ist etwas übersichtlicher :-) Siehe auch Form aus Kohärenz

Unterteilt man das Medium in 100 Schichten, so bekommt man 100 Elementarwellen, die rechts der eingezeichneten Hilfsgeraden nach rechts und links der Hilfsgeraden nach links laufen. In der nebenstehenden Momentaufnahme sind die Wellen gestapelt dargestellt. Tatsächlich interferieren alle Wellen (längs der z-Achse). Entscheidend für das Resultat ist ihre Phasenbeziehung: In einem homogenen Medium (wie hier vorausgesetzt, oder im Vakuum) interferieren die Elementarwellen nur in Vorwärtsrichtung konstruktiv, löschen sich also in alle anderen Richtungen aus: "kohärente Vorwärtsstreuung". Ist das Medium nicht homogen (ändert sich der Brechungsindex in Abständen, die nicht wesentlich größer sind als die Wellenlänge), tritt Streuung mit Richtungsänderung auf (also die "normale Streuung"), weil die Kohärenz verloren geht.

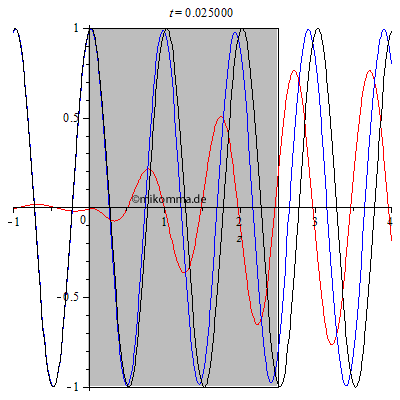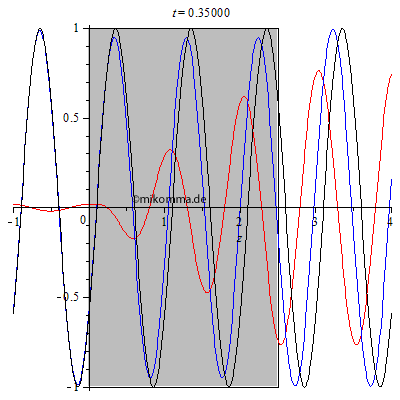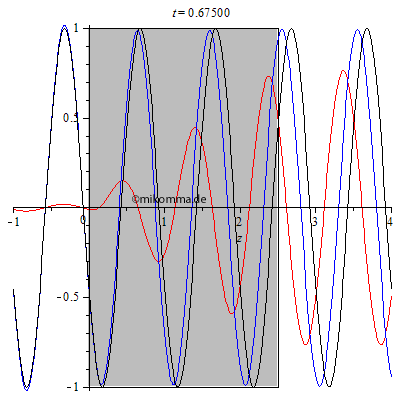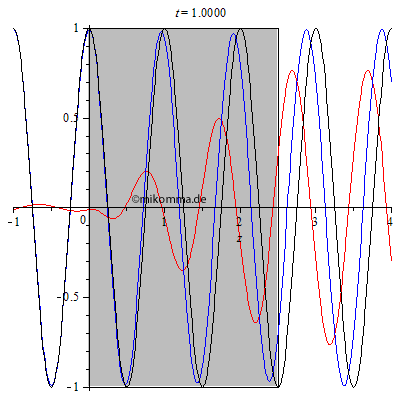
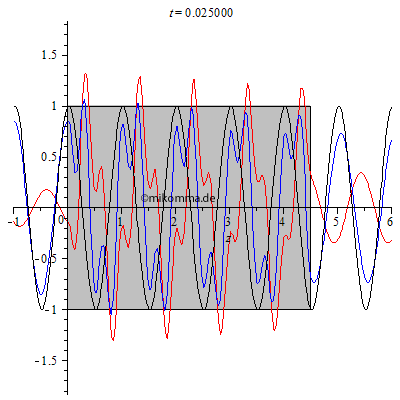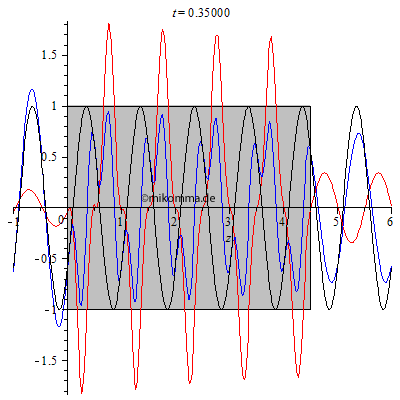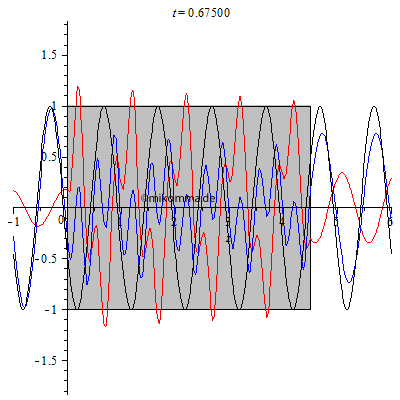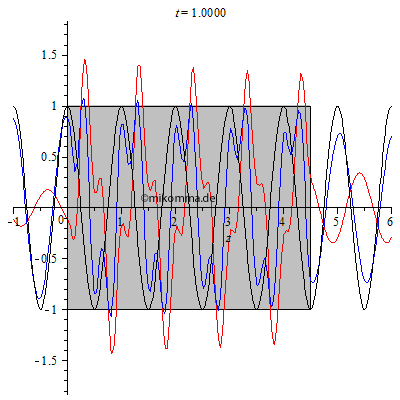
Für die folgenden Darstellungen gilt: Die Primärwelle ist schwarz dargestellt. Die gestreute Welle rot und die resultierende (primär + gestreut) blau. Alle Wellen werden komplex berechnet, die Darstellungen zeigen den Realteil.

Wir beginnen mit einem kleinen Brechungsindex n = 1.05: Wie zu erwarten baut sich eine gestreute Welle im Medium auf und ein kleiner Teil wird reflektiert. Die Überlagerung der gestreuten Welle mit der Primärwelle ergibt hinter dem Medium (rechts) eine verzögerte resultierende Welle. Man vergleiche " Form aus Kohärenz"!
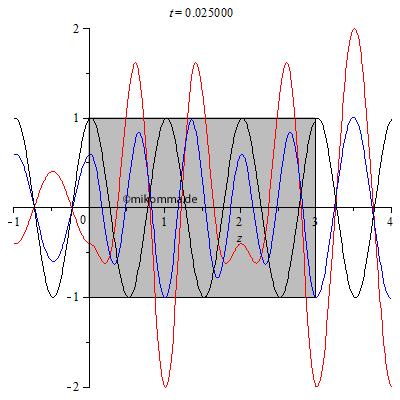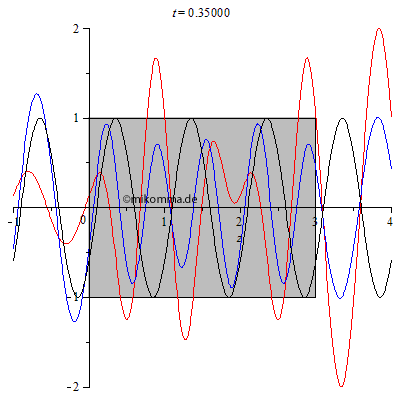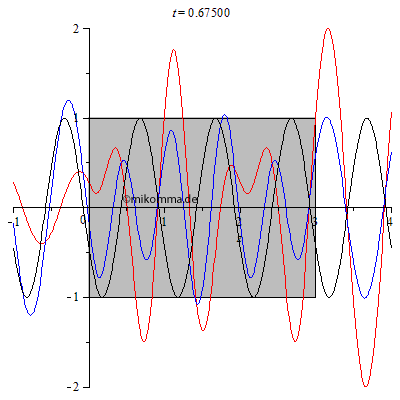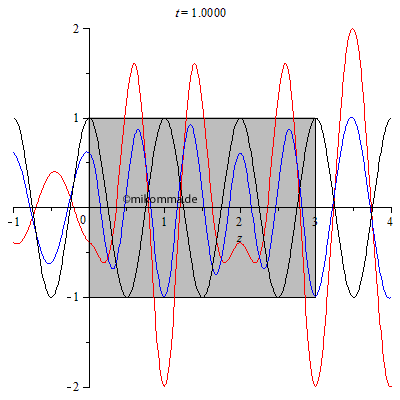
Bei einer Brechzahl von n = 1.5 und der Dicke des Mediums d = 3 wird wesentlich mehr reflektiert und es bildet sich links vom Medium eine "stehende Welle mit Schwebung". Im Medium ergibt sich aber nicht das Bild, das man mit dem iterativen Ansatz von oben bekommt, was diesen Ansatz als phänomenologisch enttarnt: Die landläufige Vorstellung der Sinuswelle mit verkürzter Wellenlänge im Medium trifft eben nicht zu, zumindest nicht, wenn das Medium nur drei Wellenlängen dick ist. Aber hinter dem Medium (rechts) stimmt jedenfalls die Verzögerung der resultierenden Welle gegenüber der Primärwelle! Aber was ist mit den Amplituden der gestreuten Welle im Medium und hinter dem Medium? Sie ist größer als die Amplitude der Primärwelle! Kein Grund zur Beunruhigung: 1. Die Animation zeigt den Realteil der Wellen (siehe auch unten Methode). 2. Das Modell der erzwungenen (ungedämpften) Schwingung geht davon aus, dass der Resonator dem Erreger (Primärwelle) keine Energie entzieht. (Siehe auch R.P.F. Gl. 31.2.)
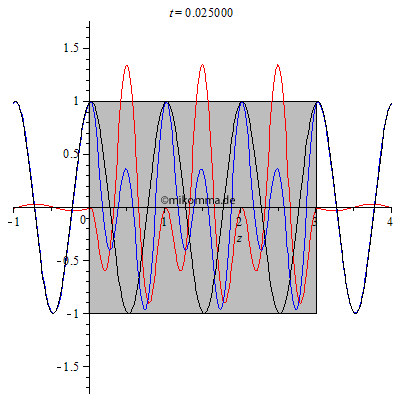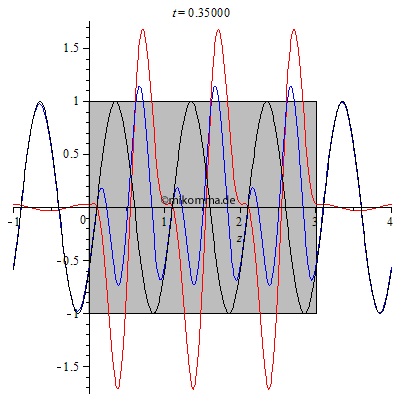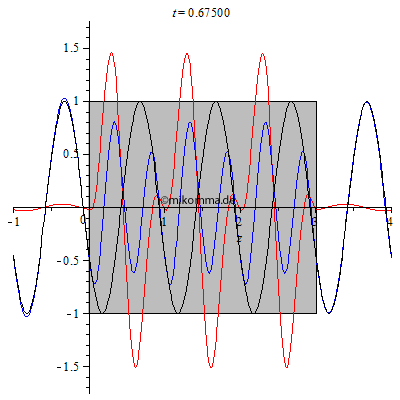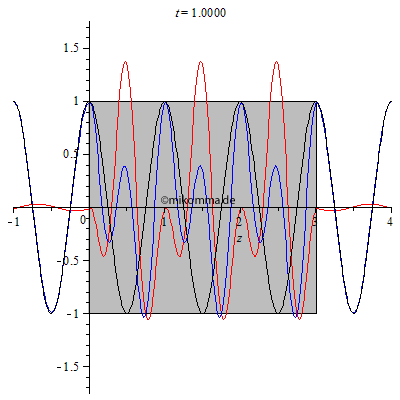
Hier ist noch ein interessanter Spezialfall, bzw. ein Test für die Gültigkeit des Modells: Brechzahl n = 2, Dicke des Mediums d = 3.005. Was ist daran speziell? Im Medium gibt es bei passender Wahl der Parameter eine stehende Welle. Die Dicke des Mediums wurde absichtlich nicht ganz passend gewählt (3.005 statt 3), um zu veranschaulichen, dass in diesem Fall (nicht exakte Abstimmung) ein Teil der gestreuten Welle aus dem Medium entkommt (vorwärts und rückwärts). Diesen Effekt verwendet man z.B. bei der Entspiegelung von Linsen.
Neben der kohärenten Streuung gibt es in realen Medien immer auch Absorption, wenn die Frequenz der Primärwelle nahe bei der Frequenz einer Absorptionslinie der Atome des Mediums liegt. Man kann diese Absorption durch den Koeffizienten k im komplexen Brechungsindex n' = n*(1 - i* k) berücksichtigen. Nebenstehende Animation wurde für d = 4.5, n = 3 und k = 0.005 berechnet und zeigt das erwartete exponentielle Abklingen der gestreuten und resultierenden Welle (die Primärwelle ist hier nur als Referenz ohne Abschwächung dargestellt). Es findet keine Reemission statt (die auch nicht kohärent sein könnte), sondern die Transparenz des Mediums wird kleiner (bis zur Undurchsichtigkeit). Darüber hinaus kann die primäre Welle durch inkohärente Streuung (z.B. Rayleigh-Streuung) geschwächt werden. Beide Prozesse (Absorption und inkohärente Streuung) können aber nur die Intensität und nicht die Phase verändern. Siehe auch: Brechungsindex und Lichtstreuung

Phasengeschwindigkeit und Gruppengeschwindigkeit

Eine unendlich ausgedehnte Welle kommt nur in theoretischen Ansätzen vor. Was wird aus Feynmans Ansatz, wenn man ein Wellenpaket verwendet?

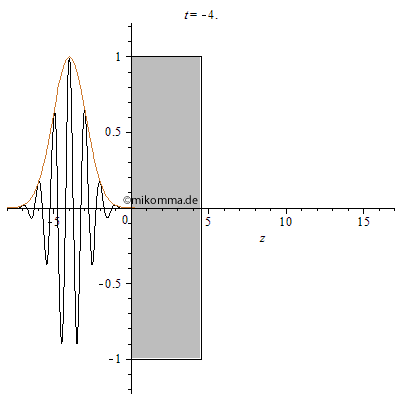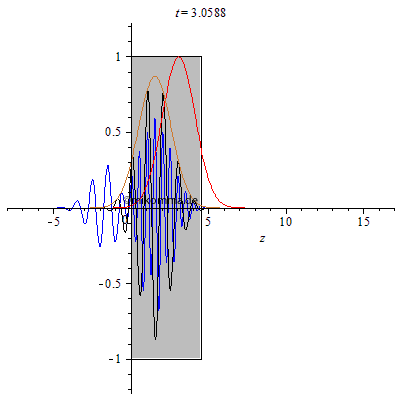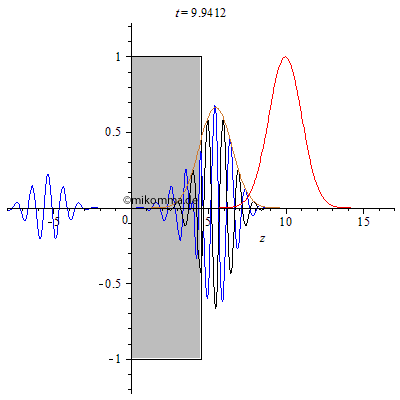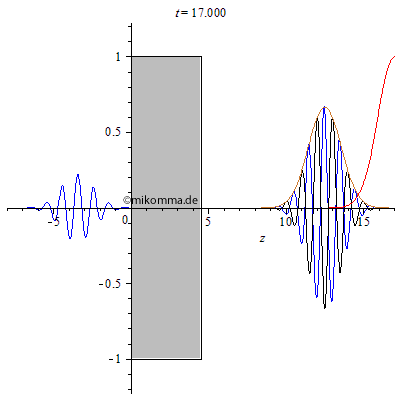
Für die Brechzahl n = 2 (in dieser Näherung frequenzunabhängig) und die Dicke des Mediums d = 4.5 sieht das etwa  so aus: Aus der Primärwelle (schwarz, Einhüllende braun) wird "eine resultierende Welle" (blau). Hinter dem Medium ist die Primärwelle mit der Einhüllenden des transmittierten Pakets (braun) als Referenz dargestellt (Phasenverschiebung zur transmittierten Welle 180° bei den gewählten Parametern). Die rote Einhüllende zeigt die Bewegung des Pakets im Vakuum zum Vergleich. Die resultierende Welle spaltet sich in der verwendeten Näherung in drei Teile auf: Durchgehendes Paket, vorne und hinten reflektiertes Paket (Mehrfachreflexionen wurden also nicht berücksichtigt). Anmerkung: die Näherung "frequenzunabhängige Brechzahl" gilt nur für schwach dispersive Medien.  Im allgemeinen Fall muss man die Dispersion berücksichtigen.

Also so falsch kann Feynmans Ansatz (und Huygens' Prinzip) nicht sein!

1. Die Reflexion des Pakets an der vorderen und an der hinteren Grenzschicht ergibt sich "quasi von selbst".

2. Das Paket hat im Medium eine kleinere Gruppengeschwindigkeit.

Neuerdings macht man ähnliche Experimente sogar mit einzelnen Photonen! Allerdings sind dort die Schichten etwas trickreicher angeordnet, so dass das Photon sogar "superluminal tunnelt".

Nun werden Sie fragen: "Wie kann ein Photon nach mehrfacher Aufspaltung am Stück absorbiert werden?" Fragen Sie mich etwas Leichteres! Aber sobald ich es weiß gibt es natürlich eine Animation zu diesem Quantensprung!

Die obigen Ausführungen bedeuten nicht, dass es "kohärente Absorption und Reemission" von Photonen nicht gibt. Mit geeigneten Vorkehrungen kann man heute Licht sogar fast zum Stillstand in geeigneten Medien bringen. Das hat aber nichts mit dem Durchgang von Licht durch Glas oder Wasser zu tun.

Methode

In obigen Darstellungen ist nur der Realteil der komplexen Amplitude (Feldstärke) dargestellt. Was sich "hinter der Bühne" abspielt, lässt sich am besten am Beispiel des Wellenpakets veranschaulichen.

Wellenpaket komplex: Hier ist eine 3D-Veranschaulichung der komplexen Amplitude der resultierenden Welle für n = 2 und d = 2.8 (der Realteil ist nach rechts hinten abgetragen, der Imaginärteil nach oben).
Oder ist die 2D-Darstellung doch besser? 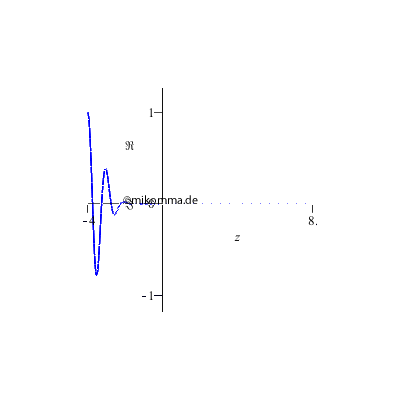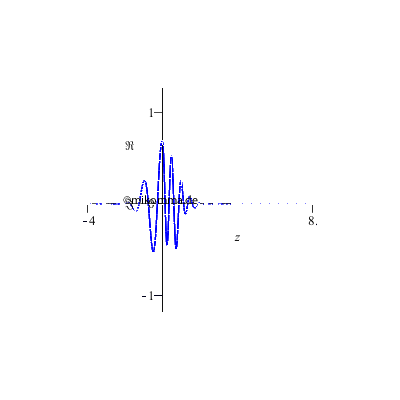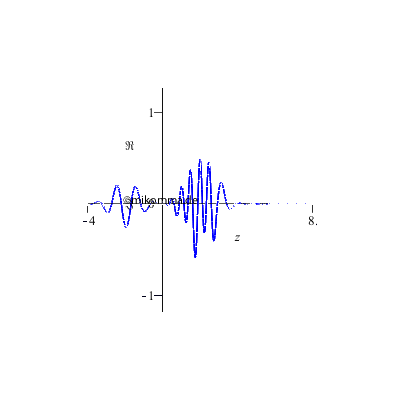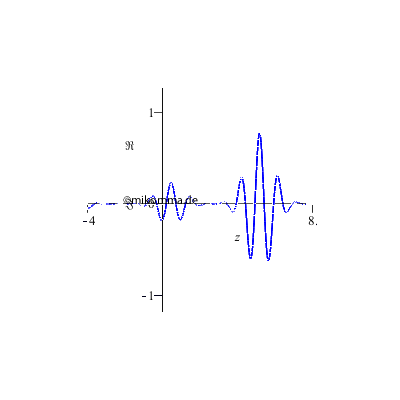Alles nur eine Frage der Perspektive,...	Oder so? 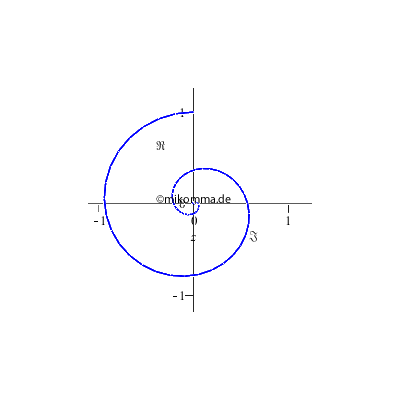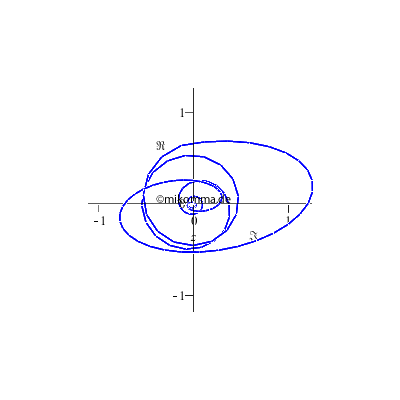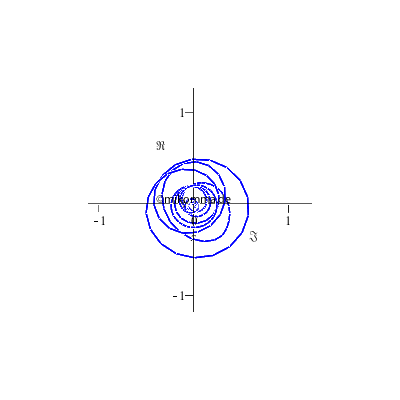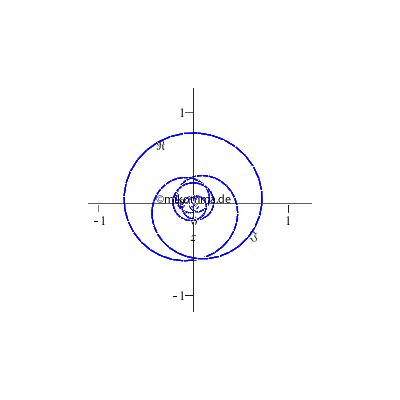die sich im Maple-Worksheet natürlich interaktiv einstellen lässt...
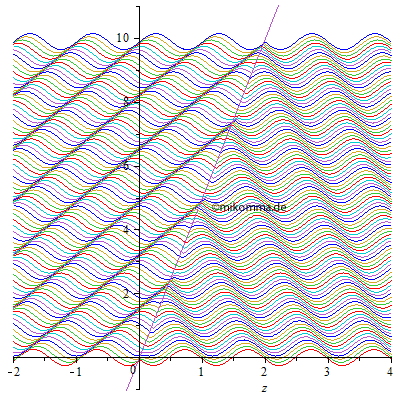
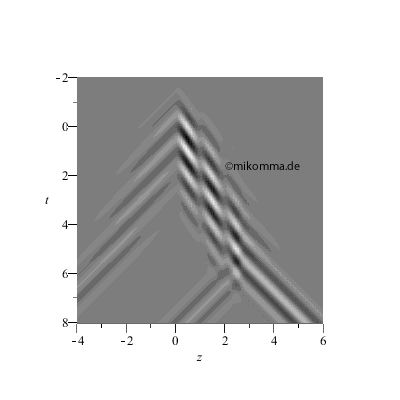
Hier ist noch eine Art der Darstellung. Das z-t-Diagramm verschafft Überblick:
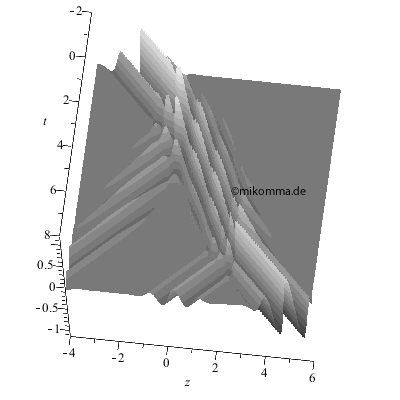
Realteil der resultierenden Welle (Primärwelle + Streuwelle) 3D. Ein Bild der Animation von oben entspricht einem Schnitt parallel zur z-Achse.	Das Ganze von oben: An den hellen Punkten sieht man die Interferenz der rückwärts laufenden Wellen mit den vorwärts laufenden.
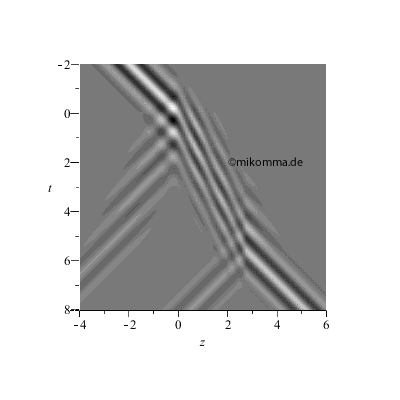
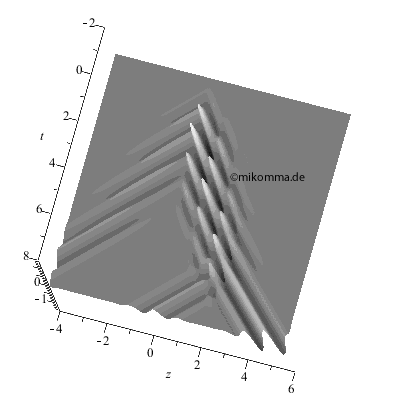
Die Streuwelle alleine...	Die Einhüllende der Huygensschen Elementarwellen läuft nur rückwärts, wenn die Ausbreitung der Elementarwellen gestört wird.