Dispersion

Wenn die Ausbreitungsgeschwindigkeit (Phasengeschwindigkeit) von Wellen von ihrer Frequenz abhängt, spricht man von Dispersion. Die bekannteste Erscheinung von Dispersion ist der Regenbogen: durch die unterschiedliche Ausbreitungsgeschwindigkeit der Lichtwellen in Wasser werden verschiedene Farben beim Übergang von Luft zu Wasser (und zurück) unterschiedlich stark gebrochen.

Wenn die Ausbreitungsgeschwindigkeit für große Frequenzen (blau) kleiner ist als für kleine Frequenzen (rot), spricht man von "normaler Dispersion", im umgekehrten Fall von "anomaler Dispersion".

Es gibt eine Vielzahl von Möglichkeiten, "Dispersionsrelationen", also den Zusammenhang von Ausbreitungsgeschwindigkeit c, der Wellenlänge λ und der Frequenz f, zu formulieren. Die bekannteste ist c(f) = λ∙f. Wenn c(f) = c konstant ist, liegt keine Dispersion vor (z.B. Licht im Vakuum).

Für die  rechnerische Untersuchung ist es bequemer, die Dispersionsrelation in der Form  ω = k∙c(k) zu verwenden. Darin ist  ω = 2πf die Kreisfrequenz und k = 2π/λ die Wellenzahl.

In realen Medien kann c(k) eine recht komplizierte Funktion sein, die überdies von vielen Parametern (Materialkonstanten und Art der Welle) abhängt. Um das Wesentliche darzustellen, werden auf dieser Seite zwei Ansätze ("mathematische Medien") gezeigt:

• 1. Näherung: c(k) ist eine lineare Funktion von k.

• 2. Näherung: c(k) ist eine quadratische Funktion von k. 

1. Näherung

Normale Dispersion: Die Phasengeschwindigkeit c(k) (grün) nimmt mit der Wellenzahl k ab. Die Kreisfrequenz ω = k∙c(k) (goldbraun) hat eine negative Krümmung (violett) und ist nicht proportional zu k wie im dispersionsfreien Fall (rot). Die Gruppengeschwindigkeit dω/dk (blau) ist kleiner als die Phasengeschwindigkeit.
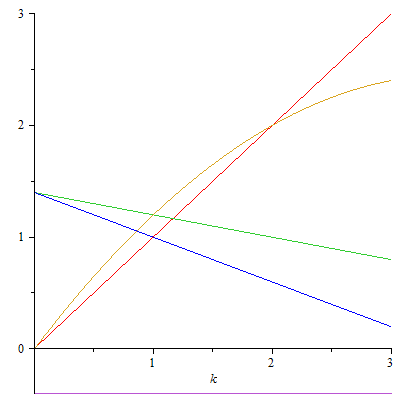
Anomale Dispersion: Sinngemäß. Alles klar?
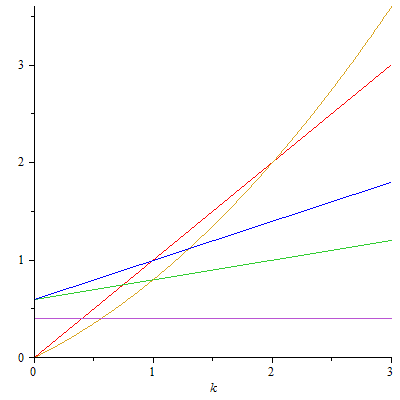
Dass sich verschiedene Wellen in verschiedenen Medien mit unterschiedlicher Geschwindigkeit ausbreiten, beschert uns zwar den schönen Regenbogen, ist aber ansonsten nicht weiter spannend. Lässt sich der Bogen etwas weiter spannen? Wie wäre es mit der Überlagerung zweier Wellen unterschiedlicher Frequenz?
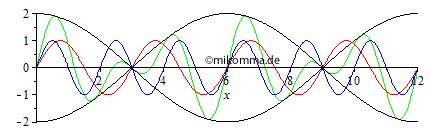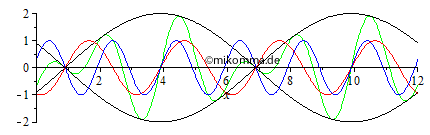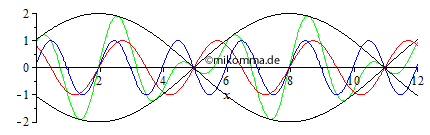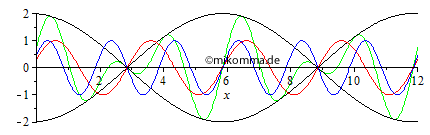
Ohne Dispersion läuft die blaue und die rote Welle mit der gleichen Geschwindigkeit wie ihre Überlagerung (grün). Auch die Einhüllende (schwarz) der Wellengruppe hält sich an die "Richtgeschwindigkeit". Das ist nicht gerade spannend, aber mit der Überlagerung bekommen wir zumindest eine Schwebung. Lässt sich die Spannung steigern?
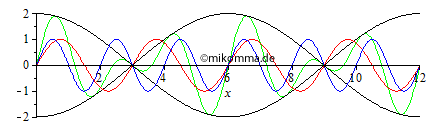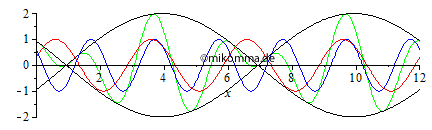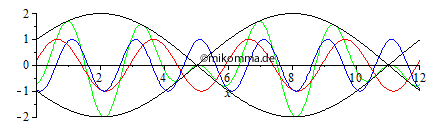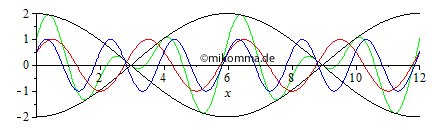
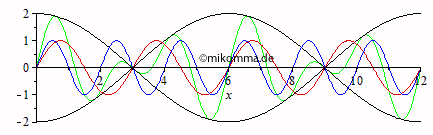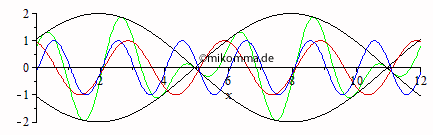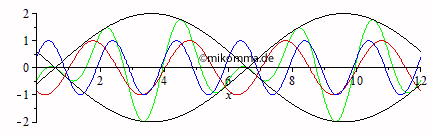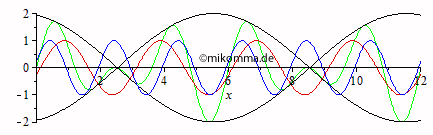
Normale Dispersion Rot überholt grün, grün überholt blau und blau überholt schwarz (Darstellung mit gleicher Gruppengeschwindigkeit wie ohne Dispersion). Das ist doch schon etwas spannender!
Anomale Dispersion "Sinngemäß"! Anmerkung: Die Animationen wurden so erstellt, dass die Geschwindigkeit der resultierenden Welle (grün) in beiden Animationen gleich ist. Die Gruppengeschwindigkeit ist dann bei anomaler Dispersion doppelt so groß wie bei normaler (in diesem Beispiel).

Tipp: Die Wiedergabe der Animationen hängt vom Browser und der Grafikkarte ab. Ggf. das Fenster so klein machen, dass nur zwei Animationen zu sehen sind, und die Seite neu laden.

Wenn man die Animationen so einrichtet, dass sich die Wellengruppe in beiden Fällen (normale und anomale Dispersion) mit gleicher Geschwindigkeit auf dem Bildschirm bewegt, erhält man:

Normale Dispersion
Anomale Dispersion

Wellenpakete

Überlagert man nicht nur zwei Wellen, sondern "beliebig viele", erhält man Wellenpakete.

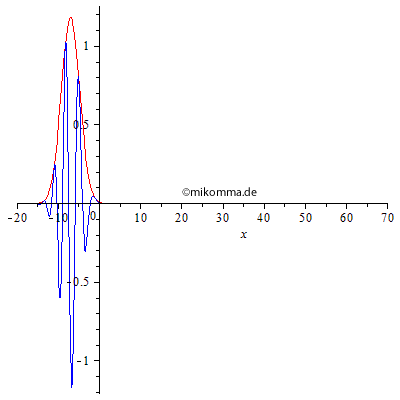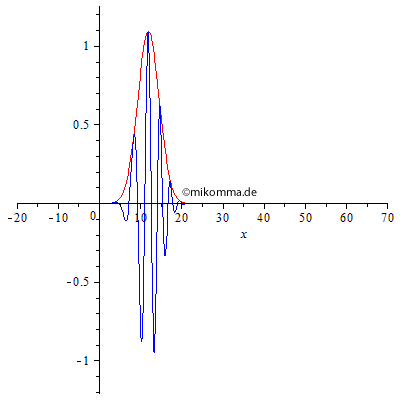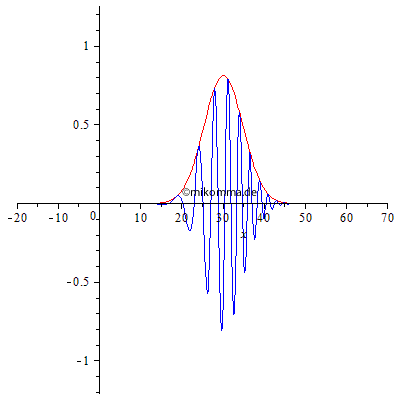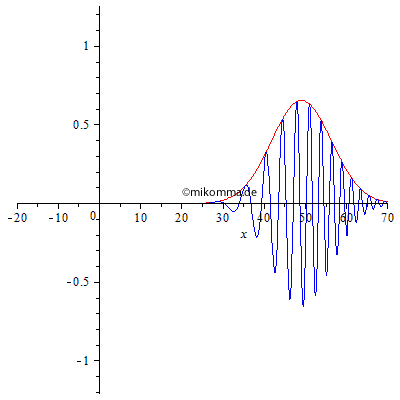
Das Standardbeispiel ist das "Gauß-Paket", also die Überlagerung von Wellen aus einem kontinuierlichen Spektrum (k) mit Gaußverteilung. Mit der hier verwendeten Näherung (c ~ k) ist die Einhüllende (rot) wieder ein Gauß-Paket, allerdings mit veränderlicher Breite, die zum Zeitpunkt (hier t = 0) minimal ist: das Paket zerfließt (bildet sich aber auch). Normale Dispersion: Die Gruppengeschwindigkeit ist kleiner als die (mittlere) Phasengeschwindigkeit der blauen Welle. Langwellige Anteile überholen kurzwellige (Chirp).
Anomale Dispersion: Sinngemäß... Übrigens: so verhalten sich Materiewellen(pakete) auch schon im Vakuum, siehe "Moderne Physik mit Maple" Wellenpakete.
2. Näherung
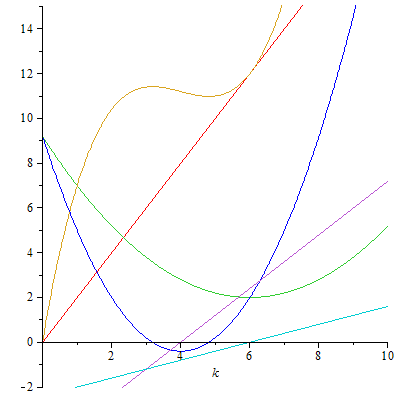
Die Phasengeschwindigkeit c(k) ~ k² (grün) hat ein Extremum (Nullstelle der Geraden in türkis). Die Kreisfrequenz ω = k∙c(k) (goldbraun) ändert die Krümmung (violett) und ist nicht proportional zu k wie im dispersionsfreien Fall (rot). Die Gruppengeschwindigkeit (blau) kann kleiner oder größer als die Phasengeschwindigkeit sein (und auch negativ, jedenfalls in diesem Beispiel :-).
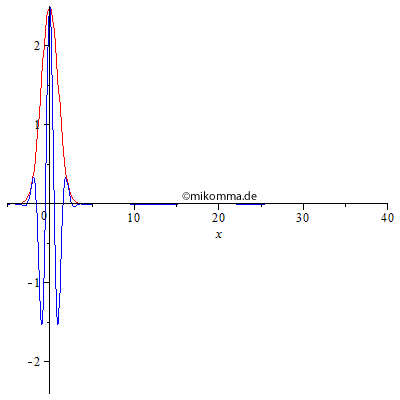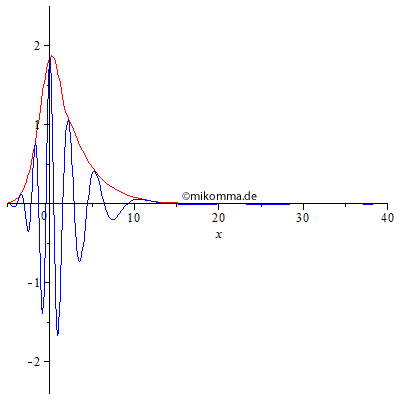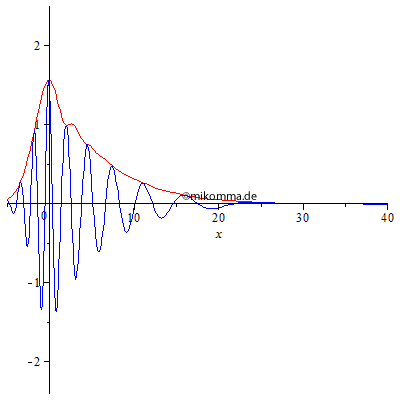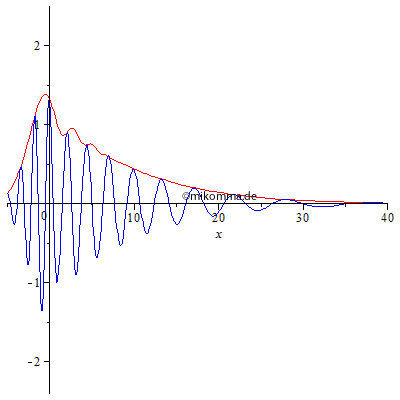
Nun bleibt ein Gaußpaket im Wellenzahlraum kein Gaußpaket im Ortsraum. Bei geeigneter Wahl der Parameter kann man sogar "stehende Wellenpakete" erzeugen, die allerdings mit Chirp zerfließen.

Nimmt man nicht ein kontinuierliches Spektrum, sondern ein diskretes (hier mit äquidistanten Linien), so erhält man sogar eine Folge von Paketen. Siehe auch Frequenzkamm. Alles nur Maple-Spielerei? Ja - auch. Aber solche Experimente werden inzwischen mit Laserpulsen und sogar mit einzelnen Photonen gemacht!