Die Formel für die Wasserstoffwellenfunktionen lautet:

In den folgenden Darstellungen wird die mit r multiplizierte Wahrscheinlichkeitsdichte verwendet. In dem Zeitfaktor ist das Wirkungsquantum h gleich 1 gesetzt und die Längeneinheit ist der Bohrsche Radius a ₀. (In Realexperimenten verwendet man nicht Wasserstoff, sondern z.B. Rubidium. Dann muss noch die Kernladungszahl berücksichtigt werden.)

Für kreisförmige Rydbergatome ist l = m = n-1, wodurch die Formel drastisch vereinfacht wird:

Dabei ist N ein von den Quantenzahlen abhängiger Normierungsfaktor und R die Radialfunktion (die von r abhängigen Faktoren in der allgemeinen Formel ohne den Faktor r am Ende). Von den Legendrepolynomen P bleibt nur eine Potenz (l) des Sinus vom Polarwinkel übrig, d.h., das Elektron ist für große l "praktisch" nur in der "Äquatorebene" des Atoms anzutreffen.

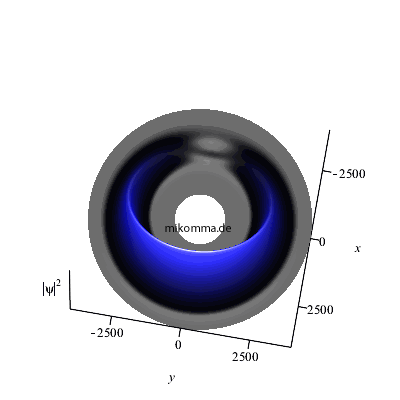
Für l = n-1 bleibt vom Laguerrepolynom L nur eine Konstante übrig und die Radialfunktion hat nur ein Maximum (und keine Nullstellen).  Nebenstehend sind die mit r multiplizierten Radialfunktionen abgebildet, und zwar für die Quantenzahlen n = 50 (rot) und n = 51 (blau). Zum Vergleich die Radialfunktionen für n = 10 und 20 (schwarz). Für r ist auf der Abszisse n2, also die Vielfachen von a 0 abgetragen. Man sieht: für große Quantenzahlen hält sich das Elektron nicht an die von Bohr ausschließlich erlaubten Bahnen, sondern vagabundiert lustig über alle möglichen "stationären Zustände" (etwa von n= 42 bis n=60) und verbotene Zonen (und zwar kontinuierlich!), so dass es vom 2000-fachen bis zum 4000-fachen Bohrschen Radius anzutreffen ist. Die Bezeichnung "kreisförmiges Atom" ist also stark vereinfachend. Bemerkenswert ist vor allem, dass sich die "Aufenthaltsbereiche" mit benachbarten Quantenzahlen fast vollständig überlappen. Wenn also ein Elektron "nicht genau weiß", zu welcher Bohrschen Bahn es gehört, kann es auch beide nehmen: Schrödingers Elektron! Diese Schrödinger-Elektronen leben in Rydbergatomen sehr lange (Millisekunden) und man kann sie mit Mikrowellen nicht nur von einer "Bohrschen Bahn" zur anderen schieben, sondern auch die Phase ihres Zustands verändern - und messen! Mehr dazu später.
Wir sollten uns also um die Phase dieser Zustände (die man nun wieder als "Superpositionszustände" neu entdeckt hat) kümmern. Sie steht in der Exponentialfunktion:
Hier ist der Realteil (nach oben über der "x-y-Äquatorebene des Atoms" abgetragen) des azimutalen Anteils dargestellt für n = 50, also m = 49 (bitte nachzählen :-).	Wenn man noch den Zeitfaktor berücksichtigt, bewegt sich der Realteil des "stationären Zustands". Die Darstellung des Betragsquadrats würde natürlich weder eine azimutale Struktur noch ihre zeitliche Veränderung zeigen.
Was geschieht, wenn "man zwei benachbarte Zustände überlagert" - rein rechnerisch, oder wenn das Elektron nicht genau weiß, ob es zu n = 50 oder n = 51 gehört?
Die Quantenzahlen m unterscheiden sich um 1. Azimutal gibt es also auf einer Seite ein Minimum und auf der anderen ein Maximum des "Superpositionszustandes": Kreisförmige Schwebung, sowohl im Realteil...	als auch im Betragsquadrat. Das bedeutet aber, dass das Elektron mit dem positiven Kern (in der Mitte zu denken) einen elektrischen Dipol bildet.
Bewegt sich etwas? Ja - das Elektron! mit seinem Realteil (und Imaginärteil)	und natürlich auch dem Betragsquadrat!
Der elektrische Dipol rotiert also, und zwar mit der Schwebungsfrequenz (für Rubidium etwa 51GHz) der beiden "stationären Zustände", oder mit der Gruppengeschwindigkeit.	Anders ausgedrückt: Durch die Überlagerung der Zustände, oder beim Übergang von einem "stationären Zustand" zum anderen, wird das Elektron zu einem lokalisierbaren Wellenpaket (sonst könnte es ja auch nicht strahlen :-).
Hier ist noch eine andere Art der Darstellung: Die Überlagerung wurde nur für n = 48 bis n = 52 berechnet. Außerhalb und innerhalb dieses Bereiches sind die "stationären Zustände" zu sehen. Die Animation läuft im Sekundentakt, damit man besser verfolgen kann wie die "Zahnräder ineinander greifen". Natürlich ergeben sich durch die Wahl der Zeitschritte (also der "Messung") stroboskopische Effekte. Das Verhältnis der mittleren Frequenz der beiden "stationären Zustünde" und der Übergangsfrequenz (= Schwebungsfrequenz) ist etwa n/2 und nicht ganzzahlig.

Einmal mehr ist von einem Quantensprung weit und breit nichts zu sehen. Rydbergatome haben eine sehr hohe Lebensdauer (> 10ms), weil die abgestrahlte Leistung sehr klein ist. Die abgestrahlte Leistung ist einerseits proportional zum Quadrat der Beschleunigung des Elektrons. Weil die Schwebungsdauer proportional zu n³ ist und der mittlere Bahnradius proportional zu n², ist also die Strahlungsleistung proportional zu n^-8.
Andererseits ist die mittlere Strahlungsleistung gleich der abgestrahlten Energie dividiert durch die Lebensdauer. Also ist die Lebensdauer proportional zu n⁵.

Würde man das Atom sich selbst überlassen, so würde also das Elektron "in aller Seelenruhe" und unter Missachtung aller verbotenen Zonen von energetisch höheren zu niedrigeren Zuständen übergehen und dabei eine Spektrallinie nach der anderen abstrahlen, siehe auch. Aber es kommt noch besser:

Setzt man das Atom in einen gut verspiegelten Hohlraum, so kann es die abgestrahlte Energie wieder absorbieren und oszilliert zwischen zwei benachbarten Zuständen, wenn der Hohlraum gut abgestimmt ist: Rabioszillationen, etwa um das Millionenfache langsamer als die Strahlungsfrequenz, also 51kHz im genannten Beispiel.

Es kommt aber noch besser: Durch gezielte Einstrahlung von Mikrowellenpulsen, kann man das Elektron nach Belieben hin- und herschieben (energetisch, aber auch räumlich). Auf den unteren Zustand oder den oberen oder eine Superposition. Wenn man das zweimal macht, hat man (mit geeigneten Pulsen) ein Ramsey-Interferometer, bei dem die Pulse wie Strahlteiler wirken. Verschiebt sich zwischen den "Strahlteilern" (Ramsey-Zonen) die Phase des "präparierten Zustands", so ändert sich die Intensität an den Ausgängen des Interferometers.

Am besten wäre es natürlich, wenn man jetzt noch einen Phasenschieber hätte. Aber keine Sorge - auch das geht und man bekommt dafür sogar den Nobelpreis, denn mit diesem Phasenschieber kann man ein Photon nachweisen, ohne es zu absorbieren!

Und wie geht das (mit dem Phasenschieber)? Wenn ein Atom durch einen Hohlraum fliegt, der verspiegelt ist und auf die Übergangsfrequenz zweier Niveaus richtig abgestimmt ist, so verschieben sich die Niveaus (light shift). Ein Beispiel mit den Zahlen aus "Quantum jumps of light recording the birth and death of a photon in a cavity", Sébastien Gleyzes, ..., Serge Haroche, doi:10.1038/nature05589 (Hochachse: Kreisfrequenz in Hz, Zeitachse in Sekunden):

Wenn der Hohlraum wirklich leer ist (elektromagnetisches Vakuum, Anzahl der Photonen n = 0), wird nur das obere Niveau (rot) angehoben. Das untere Niveau (blau, auf der t-Achse) bleibt unverändert. Achtung: in diesen Darstellungen ist der Abstand (51GHz) zwischen den (unverschobenen) Niveaus nicht berücksichtigt.	Wenn sich ein Photon im Hohlraum befindet, wird zusätzlich das untere Niveau abgesenkt.
Will man unterscheiden, ob sich ein Photon im Hohlraum befindet oder keines, so muss man die Differenz der Verschiebungen bilden...	und daraus die resultierende Verstimmung.
Wenn man alles richtig gemacht hat, sammelt das "Atom im Superpositionszustand" - also der rotierende Dipol - bei der Passage durch den Hohlraum gerade die zusätzliche Phase π auf, die man im Interferometer braucht, um oben genanntes Experiment optimal durchzuführen. Die nebenstehende Abbildung zeigt das Zeitintegral der "Verstimmung", die dafür sorgt, dass der Dipol währen der Passage durch die "Gaußmode" etwas schneller rotiert.
Belichtet man den rotierenden Dipol mit der passenden Frequenz, so sieht die Phasenverschiebung so aus (Realteil der Wellenfunktion):	Betragsquadrat
Nebenbei gesagt: Ein Zwei-Niveau-System ist eine Realisierung eines Qubits. Sie sehen hier also wie man die Phase eines Qubits schiebt, das sich in einem Überlagerungszustand befindet :-).

Nun werden Sie fragen: "Warum spricht dann S. Haroche in seiner Nobel lecture davon, dass er Schrödingers Frage " Are there quantum jumps" positiv beantwortet hat? Fragen Sie mich etwas Leichteres! Wenn es die von Schrödinger abgelehnten instantanen Bohr/Einsteinschen Quantensprünge gäbe, könnte Haroche seine Experimente gar nicht machen.

Und weshalb heißt der Artikel "Quantum jumps of light recording the birth and death of a photon in a cavity"? Weil man nur alle Millisekunden nachschaut, ob das Photon noch im Hohlraum ist. Falls nicht, so ist es aus dem (offenen!) Hohlraum ins Vakuum außerhalb des Hohlraums "gesprungen". Nun ja - wenn ich um 12 Uhr in der Sonne auf meinem Balkon einschlafe und um 15 Uhr wieder aufwache, ist die Sonne auch weg-"gesprungen" und ich liege im Schatten. So ist das halt mit stroboskopischen Aufnahmen...