Wir kennen alle die Überlagerung zweier transversaler Schwingungen.

Eine Schwingung mit horizontaler Polarisationsrichtung (grün), die andere (rot) mit Winkel α zur ersten. Zur Vereinfachung haben hier beide Schwingungen die gleich Amplitude. Das Ergebnis (blau) hängt vom Phasenunterschied δ der Schwingungen ab und sieht als Funktion der Zeit dargestellt so aus (α = 60°):

Zwei Sonderfälle: für δ = 0	und δ = 180° ist die resultierende Schwingung linear polarisiert.
Ein dritter Sonderfall: für α + δ = 180° ist die resultierende Schwingung zirkular polarisiert.	Im Normalfall ist die resultierende Schwingung elliptisch polarisiert.
Das ist alles nichts Neues und aus der klassischen Mechanik und Elektrodynamik bestens bekannt. Für unseren "Quantenradierer" benötigen wir später noch einen Polarisationsfilter (schwarz, Winkel β zur Horizontalen). Er lässt nur die Projektion der resultierenden Schwingung auf die Richtung β durch - was auch nicht neu ist.

Es gibt nun Experimente, bei denen man hinter einen Doppelspalt Polarisationsfolien mit unterschiedlicher Richtung klebt, um damit "den Weg des Photons zu markieren". Natürlich funktioniert die Überlagerung zweier transversal polarisierter Wellen auch klassisch:

Die resultierende elektrische Feldstärke kann so angesetzt werden (x- und y-Komponente):

(1)

(2)

Das ergibt z.B. folgende Polarisationsellipsen (Kurven, die der E-Vektor im Laufe der Zeit beschreibt), wenn man den Phasenunterschied δ der beiden Schwingungen variiert:

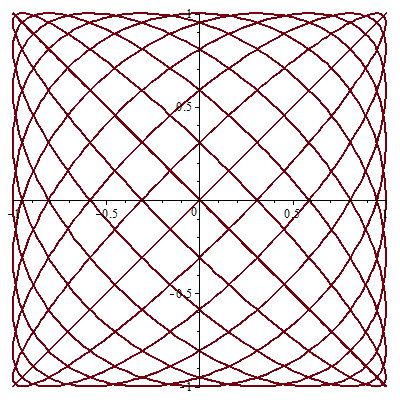α = 90°

α = (90/8)°

Die Ellipsen mit Phasenunterschied δ als Parameter liegen in einem Parallelogramm - Raute für gleiche Amplituden - und haben ihre Hauptachsen auf den Diagonalen des Parallelogramms.

Oder als Animation

Relative Orientierung α der Polarisationsrichtungen fest, Variation des Phasenunterschieds δ

Phasenunterschied fest, Variation der Polarisationsrichtung

Sind das die Heiligenscheine der Quantenradierer? Wir suchen lieber nach etwas Beobachtbarem!

Bringt man z.B. die Lichtstrahlen (oder Wellen?), die einen Doppelspalt mit Polarisationsfolien verlassen "auf einem Schirm zur Interferenz", so ergäben sich folgende Bilder, wenn man die Polarisationsellipsen sichtbar machen könnte:   

Von unten nach oben: α = 90°, 45°, 22.5° Der Phasenunterschied δ variiert in horizontaler Richtung.

Leider kann man aber diese Polarisationsellipsen nicht sichtbar machen, weil es nur Schirme, Detektoren und Atome gibt, die über die Zeit mitteln. Man sieht aber schon im obigen Bild, dass in der untersten Reihe die Amplitude der Schwingung (und damit die Intensität) "überall gleich groß" ist, während sie in der obersten Reihe stark variiert.
Man kann das auch in Animationen darstellen:

Animation links: Dies entspricht der untersten Zeile von oben, also orthogonale Polarisationsrichtungen. Auf einem Schirm sind keine Interferenzstreifen sichtbar, weil die Intensität überall gleich groß ist. In der Mitte (y = 0) hat man rechtszirkular polarisiertes Licht, dann kommt bei y = 2.5 diagonal polarisiertes Licht (von links oben nach rechts unten) und bei y = 5 linkszirkular polarisiertes Licht, usw...

Animation rechts: "Gedankenexperiment", in dem von unten (z = 0) nach oben (z = 10) der Winkel zwischen den Polarisationsrichtungen von 90° auf 0° verkleinert wird (damit es nicht langweilig wird, in Bezug auf die Vertikale :-)). Mit einer räumlichen Modulation des Lichts (spatial light modulation = SLM) kann man ähnliche Experimente auch in der Realität durchführen, sogar mit einzelnen Photonen! Im vorliegenden Fall ("Quantenradierer mit Doppelspalt") würde man also hinter einem Spalt ein Polarisationsfilter verwenden, dessen Polarisationsrichtung sich von unten nach oben kontinuierlich verändert. Damit erhielte man dann Interferenzstreifen, deren Sichtbarkeit von unten nach oben kontinuierlich zunimmt.

Für die weitere Untersuchung brauchen wir das

Zeitmittel der Intensität 

Dafür bilden wir zunächst das Quadrat des Betrags der Resultierenden und erhalten die Intensität als Funktion der Zeit

(3)

oder vereinfacht

(4)

Und integrieren über eine Periode

(5)

Für α oder δ = 90° bleibt die Intensität konstant 1. Polarisationsfilter unterscheiden nicht zwischen 0° und 180°, also

(6)

Der Faktor |cos(α)| ist nichts anderes als die Sichtbarkeit des Interferenzmusters, die alle Werte zwischen 0 und 1 annehmen kann (und nicht nur die Randwerte 0 und 1). Die Intensitätsstreifen auf dem Schirm sehen dann so aus, wenn man den Polarisationswinkel α verändert:  

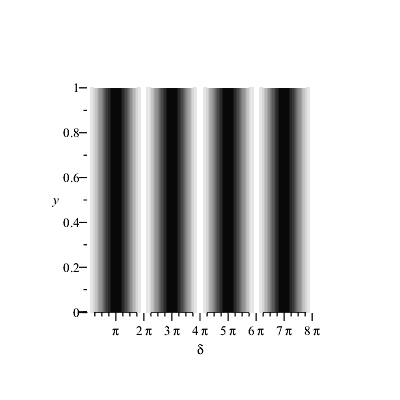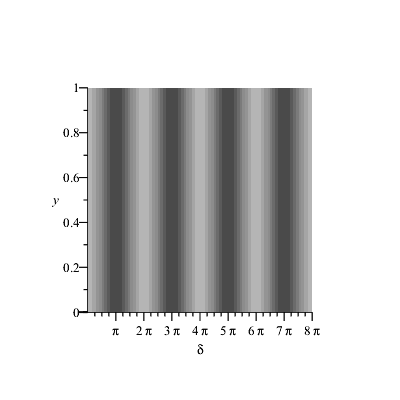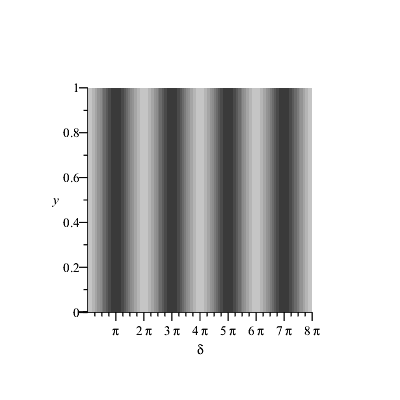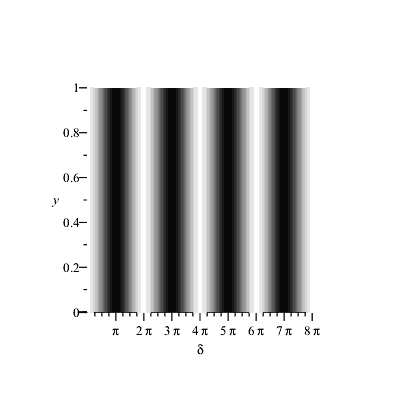
Man sagt manchmal auch "zwei senkrecht zueinander polarisierte Wellen können nicht interferieren" (Fresnel - Arago) und verwechselt dabei oft Interferenz mit Superposition. Die armen Wellen! Wenn man sich das Bild "Polarisationsellipsen auf dem Schirm" noch einmal anschaut, können die Wellen viel mehr als man sieht (und denkt): in allen Fällen sind je nach Gangunterschied alle Sorten der Polarisation vertreten, nur für α = 90° ist eben die über die Zeit gemittelte Intensität gleich groß.

Und wo bleibt nun der Quantenradierer?

Wir versuchen es mit einem dritten Polfilter, der mit der Horizontalen den Winkel β einschließt. Das liefert die mittlere Intensität

(7)

Oder nach Vereinfachung

(8)

Speziell für α = 90° ist das

(11)

Im nächsten Plot ist die voll sichtbare Interferenz (ohne Polfilter, α = 0°) rot dargestellt und für α = 90° schwarz (Sichtbarkeit = 0).
Für α = 90° (siehe Gleichung (11)) kann man das Interferenzmuster wieder sichtbar machen, wobei man für β = 45° (grün) und β = -45° maximale Sichtbarkeit erhält, allerdings bei halber Intensität. Im Gegensatz zur Änderung der Sichtbarkeit mit dem Winkel α erhält man zwei sich ergänzende Streifenmuster ("fringes" und "antifringes").

Animation der Intensitätskurve, bzw. der Streifen, wenn man den Polfilter dreht (α = 90°):

Man braucht also weder Quanten noch Radierer, um die Interferenz polarisierter Wellen zu beschreiben - das geht ganz klassisch. Aber "Licht besteht doch aus Photonen" und man kann das Experiment auch mit einzelnen Photonen machen?
Dann geht die in der Quantenfolklore übliche Interpretation etwa so: Durch die Polarisationsfolien am Doppelspalt weiß man "durch welchen Spalt das Photon gegangen ist" und erhält "Welcher-Weg-Information" und deshalb "kann das Photon nicht mehr mit sich selbst interferieren" (das arme Photon!). Nimmt man nun einen dritten Polfilter, so "radiert man damit die Welcher-Weg-Information aus" und "das Photon kann wieder mit sich interferieren".

Das ist aber nur ein weit verbreiteter Trugschluss, siehe David Ellerman "A very common fallacy...".

Kurzfassung: Wenn man mit dieser Anordnung tatsächlich eine Information über den Weg des Photons bekäme, könnte es nie mehr mit sich selbst interferieren. Man radiert also mit dem dritten Polfilter nicht Information aus, sondern Intensität, also Photonen!

Weitere Paradoxa aus der Quantenfolklore (inzwischen werden ja auch "Baukästen für Quantenradierer" angeboten):

• "Wenn das Interferenzmuster verschwindet (α = 90°), hat das Photon genau einen Weg genommen."
  Und welchen nun? Sieht man das dem Polfilter hinter einem der Spalte an?

• "Wenn das Interferenzmuster nicht völlig unsichtbar ist (α < 90°), weiß man nicht genau, welchen Weg das Photon genommen hat".
  Und wozu ist diese Information gut?

Die Quantenfolklore findet sich inzwischen auch in Abituraufgaben (nach obigem Baukastenprinzip):

"In einem Experiment werden Elektronen aus der Ruhe heraus durch eine Spannung von 1,70 kV beschleunigt und treffen senkrecht auf einen Dreifachspalt. Hinter dem Dreifachspalt wird in einer Ebene parallel dazu mit einem Elektronendetektor die Häufigkeitsverteilung gemessen. Der Spaltmittenabstand beträgt 200 nm. Der Elektronendetektor befindet sich 20,0 cm hinter dem Dreifachspalt.
• Berechnen Sie den Abstand zweier benachbarter Hauptmaxima.
• Skizzieren Sie die Häufigkeitsverteilung.
Durch eine geeignete Apparatur kann nun zuverlässig nachgewiesen werden, ob ein Elektron den mittleren Spalt passiert.
• Beschreiben und begründen Sie die dadurch entstehenden Veränderungen in der Häufigkeitsverteilung.

Lösungsvorschlag ("nur für den Dienstgebrauch" =  Cargo-Kult in Reinkultur!) zur letzten Frage:
"Die Interferenzfähigkeit des mittleren Spalts mit den äußeren geht verloren. Die beiden äußeren
Spalte bilden ein Interferenzbild eines Doppelspaltes mit doppelt so großem Spaltabstand wie der
Dreifachspalt. Überlagert wird dieses Bild mit dem Interferenzbild eines Einfachspaltes."

Hier ist noch eine Abituraufgabe:

Zitat =============================== Anfang
Der Nobelpreisträger Richard Feynman schreibt zu Doppelspaltexperimenten mit einzelnen Elektronen:
"Wir haben vorausgesetzt, dass es in unserem experimentellen Aufbau (oder sogar in dem bestmöglichen) unmöglich sein würde, genau vorherzusagen, was passiert. Wir können nur die Chance voraussagen! [. . .]

• Erläutern Sie Feynmans Aussage am Beispiel der Interferenz von Elektronen.
• Beurteilen Sie, ob die folgenden Bedingungen erfüllt sein müssen, damit beim Doppelspaltexperiment mit einzelnen Elektronen Interferenzerscheinungen beobachtbar sind:
- Der Impuls der einzelnen Elektronen muss möglichst gleich sein.
- Die Elektronen müssen mit möglichst großer Spannung beschleunigt worden sein.
- Die Apparatur muss sich im Vakuum befinden.
Zitat ============================== Ende

Nun ja: an einem "einzelnen Elektron" kann man keine Interferenzeigenschaften beobachten, sondern nur am Ensemble. Der Nobelpreisträger Feynman hat das oft genug betont. Deshalb hätte er auch nie die Frage gestellt, ob sich "die Apparatur im Vakuum befinden muss". Was soll ein Schüler auf diese Frage antworten?

1. Wenn sich die Apparatur im Vakuum befindet, gibt es auch keinen Beobachter? Weit gefehlt!
2. Wenn sich die Apparatur in Luft befindet, verglüht die Glühkathode beim Einschalten? Weit gefehlt!
3. In Luft erreichen die Elektronen den Doppelspalt nicht? Weit gefehlt!

Als Antwort wird erwartet (sinngemäß): Wenn sich die Apparatur nicht im Vakuum befindet, liefern die Luftmoleküle "im Prinzip Welcherweginformation", und das zerstört die Interferenz!

Ja - so einfach ist die Cargo-Kult-Quantenphysik-Didaktik: Man nimmt die prägnante Formulierung eines Nobelpreisträgers (und genialen Didaktikers) und bastelt daraus einen neuen Abi-Aufgabentyp (Schüler soll Nobelpreisträger interpretieren). Dann tagen Aufgabenkommissionen im Vakuum und zelebrieren ohne jegliche Weginformation im Ensemble den Cargo-Kult jährlich neu. So radiert man systematisch das Verständnis für Quantenphysik aus! Das Feynman-Cargo-Original