Elektromagnetische Wellen sind das Standardbeispiel für transversale Wellen: Die Vektoren der elektrischen Feldstärke, der magnetischen Feldstärke und der Ausbreitungsrichtung stehen paarweise senkrecht aufeinander, jedenfalls bei einer ebenen elektromagnetische Welle. Dann sollte das doch auch bei der Überlagerung von ebenen Wellen so sein?
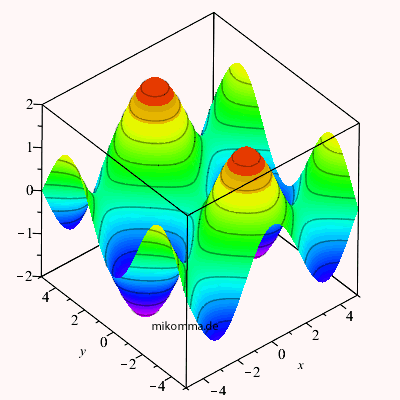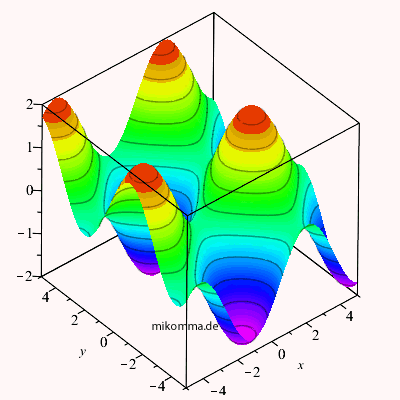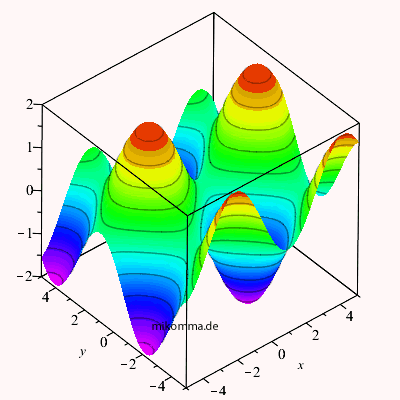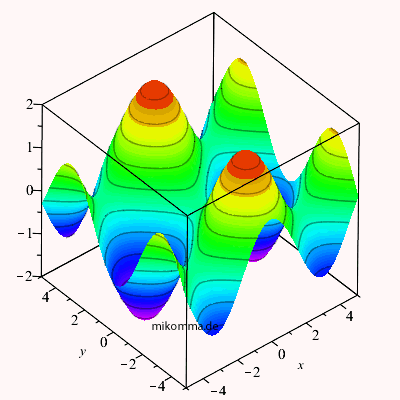
| Hier ist eine 3D-Darstellung der Amplitude zweier ebener Wellen (gleiche Amplitude, gleiche Wellenlänge), die sich in x- bzw. y-Richtung bewegen: | Und wir haben gelernt, dass sich die Wellen nicht nur "ungestört durchdringen", sondern dass sich dabei ihre Amplituden addieren: |
 |
 |
|
Die Amplitude ist ein Skalar. Obige Bilder stimmen also für
skalare Wellen. Sie stimmen auch für Vektorwellen, wenn der (Feldstärke-) Vektor
senkrecht auf beiden Ausbreitungsrichtungen steht, also in diesem Beispiel beide
Wellen "senkrecht polarisiert sind". Was passiert, wenn beide Wellen "horizontal
polarisiert" sind, also die Feldstärkevektoren in der Ebene liegen, die von den
Vektoren der Ausbreitungsrichtungen aufgespannt wird? |
|
| Hier ist eine Animation der Feldlinien und Feldstärke-Vektoren (elektrisches Feld), wenn sich zwei ebene Wellen im rechten Winkel treffen: | Hier treffen sich zwei "horizontal polarisierte" Wellen unter einem Winkel von 25° (eine davon läuft in x-Richtung). |
|
|
 |
|
Was sagt uns die
linke Animation?
Längs der
Winkelhalbierenden
(und auf
weiteren
Parallelen dazu)
schwingt das
elektrische Feld
"longitudinal",
wenn man die
Winkelhalbierende
als
Ausbreitungsrichtung
der
resultierenden
Welle nimmt.
Außerhalb der
Winkelhalbierenden
drehen sich die
Feldstärkevektoren,
nehmen also alle
Richtungen
zwischen
"transversal und
longitudinal"
an. Anmerkung: Die Feldstärke ist dort am größten, wo die Dichte der Feldlinien maximal ist. |
Was sagt uns die rechte Animation? Im Gegensatz zur linken Animation, die wohl eher ein "laufendes Interferenzmuster" darstellt als eine (einzige) "echte elektromagnetische Welle", werden hier die E-Wirbel eines Gaußstrahls sichtbar - allerdings zweigeteilt. Und die longitudinale Polarisation ist nicht sehr ausgeprägt und die Feldstärke auf der optischen Achse schwach. Aber keine Sorge: Mit einem radial polarisierten Laserstrahl kann man sogar Elektronen beschleunigen! |
Aber bitte mit B-Feld!

Die "resultierende Welle" bewegt sich hier zur Abwechslung nach vorne (im Bild unten).

