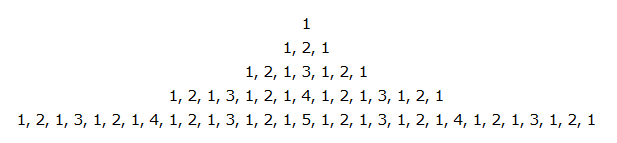|
This is where the towers of Hanoi emerge in
milliseconds! Dedicated to Harry Paul on his 91st birthday In computer science, the Towers of Hanoi (Wiki) are considered a prime example of a problem that can only be solved recursively (or iteratively). The time for calculating a certain position n thus grows exponentially with O(2n). In this article an explicit solution is presented with which one can compute any position n with the same computing time O(1). This explicit solution is used in all animations. For 10 disks, the rearrangement looks like this (the number of moves is shown at the top, with a 1 second pause for Mersenne numbers):
Suppose the monks started moving one disk per second exactly 91 years ago. Then the positions of the disks at times 91a-45s to 91a+45s look like this (the top disk (1) is moved every second move, etc.):
Or with disks: The start position 0 (exactly before 91a) is displayed 5 seconds, then it continues every second as above, i.e. with 91a-45s:
Congratulations!
© 11.02.2022, Dr. Michael Komma (VGWORT) Method: Explicit calculation of the position of the disks for a given number of moves. Computing time per position 50ms. For comparison: The time for recursive calculation of the position 91*365*24*3600 = 2869776000 is 6.7h.
Details: The standard procedure for recursively calculating the positions of the disks looks like this:
With four disks and the positions a,b and c one gets e.g.
Where 1..4 is the number of the disk (1 for the smallest) that is moved from the first (start) to the last (target) position (the middle position or park position is only listed for completeness). So "1,a,c,b" means: move disk 1 from a to b, and "2,a,b,c": move disk 2 from a to c. You can see in this example: Since the motion of the disks is cyclic, it cannot be a problem that can only be solved recursively (or iteratively). So there must be an explicit solution. In order to find this explicit solution, one only has to answer the question of how often disk j was moved if a total of n moves were made. A simple counting procedure is used to find
Visualization for five disks
Which reduces the computing time from O(2^n) to O(1).
As is known, the number of the disk that has to be moved can be calculated like this (recursion relation):
or like this (explicitly):
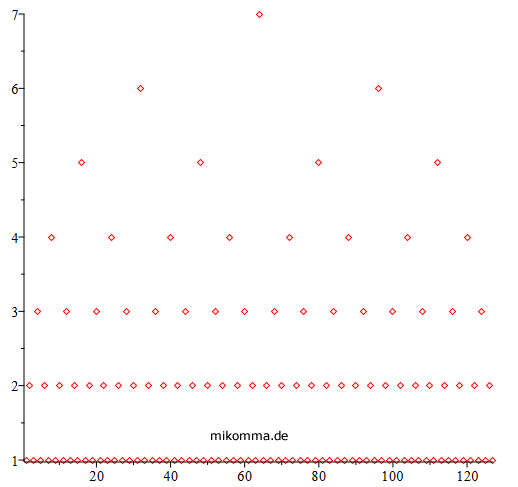
But then you don't know where the disk is. For the recursion relation one also finds representations of the type (abscissa: number of the move, ordinate: number of the disk that is being moved):
or as a tree
In particular, the tree representation is read with its branches
from top to bottom (computer trees and family trees have their roots at the top
:), so not in the order of the moves.
Download Worksheet (minimal version). See also: Weihnachten 2020 | Venuszyklus | Analemma | schielender Mond | Uhrenparadoxon | Schwebungen | Quantensprung More links: Spontane Emission | Kaskade | Photogalerie | Photonenemission | Weisskopf-Wigner Moderne Physik mit MapleHOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top |