|
Der Venuszyklus
Im Laufe von
ziemlich genau
acht Jahren überholt die Venus die Erde fünf Mal. Von der Erde aus gesehen
(geozentrisch) kann man das in einem kartesischen Koordinatensystem so
beschreiben:
Koordinaten der Venus
| > |
 |
| > |
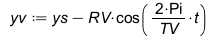 |
![Typesetting:-mprintslash([xv := `+`(xs, `*`(RV, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TV)))))))], [`+`(xs, `*`(RV, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TV)))))))])](images/Venuszuklus0_4.gif) |
![Typesetting:-mprintslash([yv := `+`(ys, `-`(`*`(RV, `*`(cos(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TV))))))))], [`+`(ys, `-`(`*`(RV, `*`(cos(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TV))))))))])](images/Venuszuklus0_5.gif) |
(1) |
Koordinaten der Sonne
| > |
 |
| > |
 |
![Typesetting:-mprintslash([xs := `+`(`-`(`*`(RE, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TE))))))))], [`+`(`-`(`*`(RE, `*`(sin(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TE))))))))])](images/Venuszuklus0_9.gif) |
![Typesetting:-mprintslash([ys := `*`(RE, `*`(cos(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TE))))))], [`*`(RE, `*`(cos(`+`(`/`(`*`(2, `*`(Pi, `*`(t))), `*`(TE))))))])](images/Venuszuklus0_10.gif) |
(2) |
ergibt
| > |
 |
 |
 |
(3) |
Konkrete Zahlen:
Bahnradien in Mio km
| > |
 |
![Typesetting:-mprintslash([RV := 108.2], [108.2])](images/Venuszuklus0_15.gif) |
![Typesetting:-mprintslash([RE := 149.6], [149.6])](images/Venuszuklus0_16.gif) |
(4) |
Umlaufdauer in Tagen
| > |
 |
![Typesetting:-mprintslash([TV := 224.701], [224.701])](images/Venuszuklus0_18.gif) |
![Typesetting:-mprintslash([TE := 365.256], [365.256])](images/Venuszuklus0_19.gif) |
(5) |
ergibt
| > |
 |
 |
 |
(6) |
Damit sieht die geozentrische Bahn der Venus für 32 Jahre so
aus
| > |
![plot([xv, yv, t = 0 .. `+`(`*`(32, `*`(TE)))]);](images/Venuszuklus0_23.gif) |
Weil das Verhältnis der Umlaufzeiten nicht exakt 13/8 ist,
schließt sich die Bahn nach 8 Jahren nicht exakt.
Animation für 8 Jahre
| > |
![display([seq(plot([xv, yv, t = 0 .. `+`(`*`(`/`(1, 40), `*`(k, `*`(TE))))], color = red), k = 1 .. 320)], insequence = true);](images/Venuszuklus0_25.gif) |
|
|
|
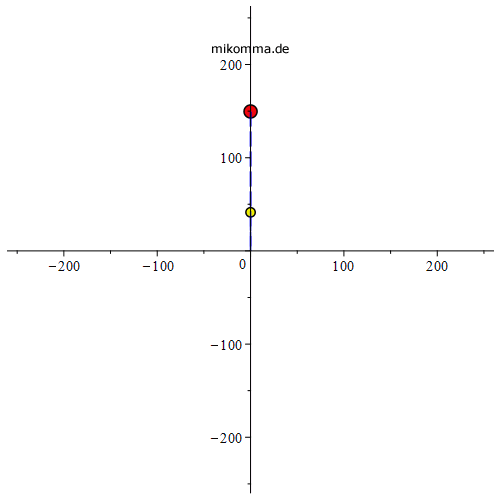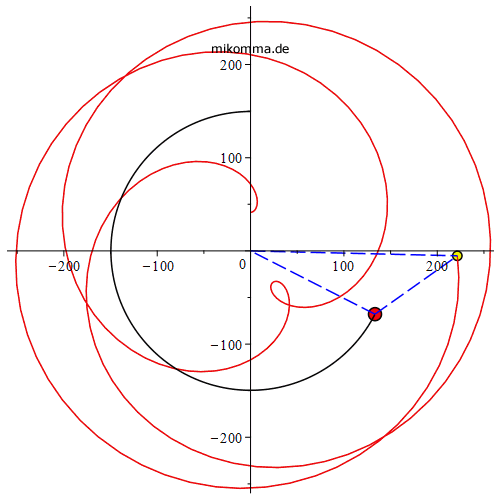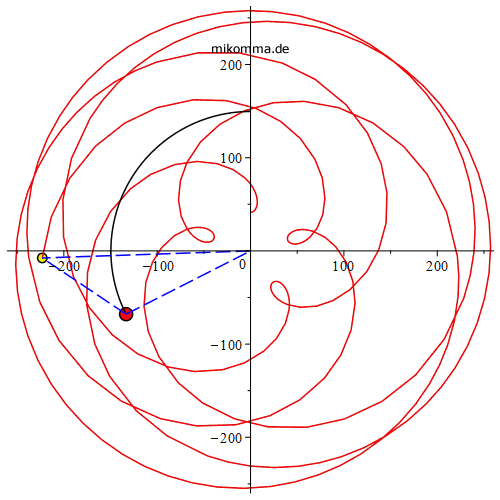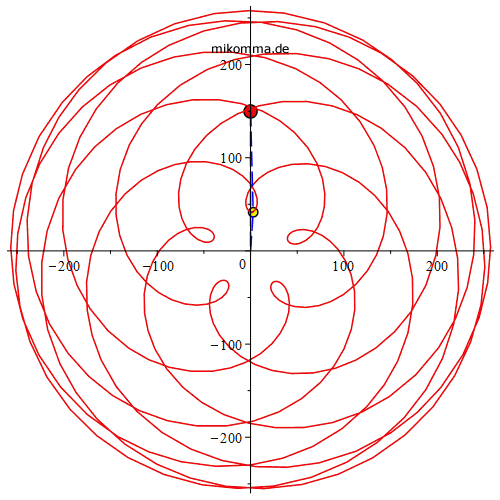
Mit Sonne (schwarze Bahn) und Verbindungslinien Erde - Sonne - Venus,
Epizyklen: |
|
geozentrisch
 |
Venus-zentrisch
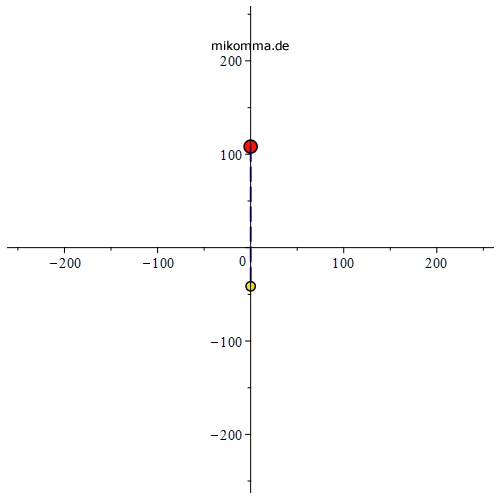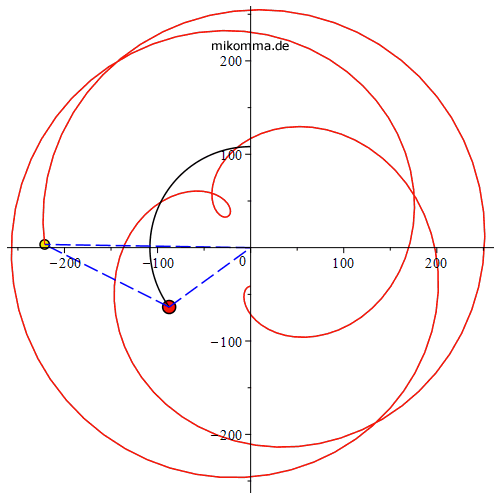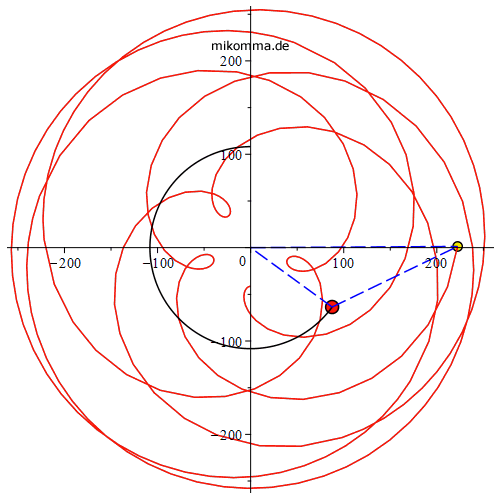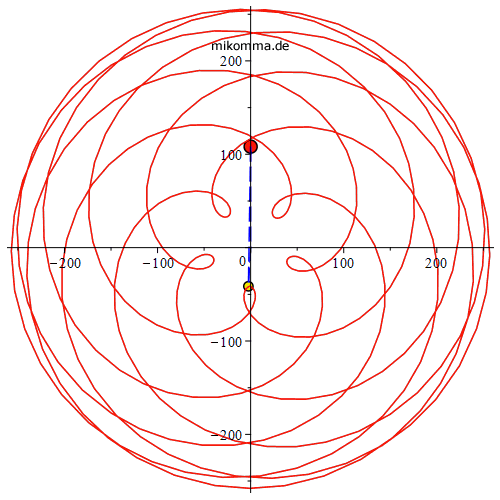 |
|
Verallgemeinerung
Man kann sich fragen, ob ein exakter Zyklus in der Konstellation
zweier Planeten die "absolute Ausnahme" ist, bzw. bei welchen Abständen exakte
Zyklen entstehen. Dazu verwendet man besser Polarkoordinaten, oder - noch
kompakter - komplexe Zahlen:
| > |
 |
 |
(1) |
Die
Bahn z ist die Überlagerung zweier Schwingung mit den Amplituden r1
und r2 (Bahnradien um die Sonne) und den Winkelgeschwindigkeiten ω1 und ω2.
Das ergibt mit dem 3. Keplerschen Gesetz und den Umlaufzeiten T1 und
T2:
| > |
 |
 |
(2) |
mit "T1 = r1 = 1"
(also z.B. T1 = 1a, r1 = 1AE) lautet dann die Bahngleichung in der
komplexen Ebene:
| > |
 |
 |
(3) |
Hier sind ein paar Beispiele (die Funktion cplz() verwendet Maples
complexplot() und im ersten Argument T2, als Bruch über der
Animation angezeigt):
Innerer Planet
![display([seq(cplz(`+`(`*`(`/`(1, 40), `*`(k))), 1, t), k = 2 .. 40)], insequence = true);](plkomimages/plkomplex_7.gif)

Äußerer Planet
![display([seq(cplz(`+`(`*`(`/`(1, 20), `*`(k))), 5, t), k = 61 .. 100)], insequence = true);](plkomimages/plkomplex_10.gif)

Und "natürlich" gibt es unendlich viele Bahnradien bzw.
Umlaufzeiten mit zyklischen Konstellationen, weil alle rationalen Zahlen
zueinander kommensurabel sind.
Die Frage ist nur: a) wie lange dauert der Zyklus? Und b) wie oft wiederholt
sich eine Konstellation innerhalb eines Zyklus?
Wir sehen uns dazu noch einmal "exakte Venuszyklen" in der
Nachbarschaft von T = 13/8 genauer an:
| > |
![display([seq(cplz(`+`(`/`(13, 8), `*`(`/`(1, 8000), `*`(k))), 15, t), k = -20 .. 20)], insequence = true);](plkomimages/plkomplex_14.gif) |
Das hat wohl etwas zu tun mit a) dem Nenner des
Bruchs und b) mit der Differenz von Zähler und Nenner?
| 