Lagrangepunkte

Lagrangepunkte, stabile Orbits und Trojaner

Eine kurze Notiz zum Dreikörperproblem.

Wie bewegt sich ein Körper im Schwerefeld zweier Massen? Um diese Frage, also das Dreikörperproblem, zu untersuchen, muss man sich zunächst mit zwei Körpern (punktförmigen Massen) beschäftigen, also mit dem Zweikörperproblem (oder Keplerproblem). Bevor man Bewegungsgleichungen aufstellt (für zwei oder drei Körper), ist es angebracht, sich ein Bild über die Potentiale zu machen:

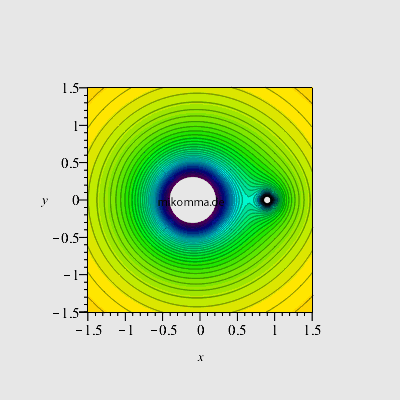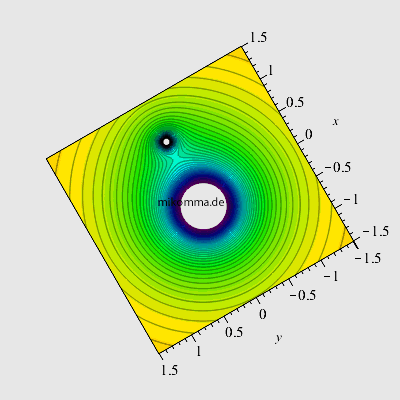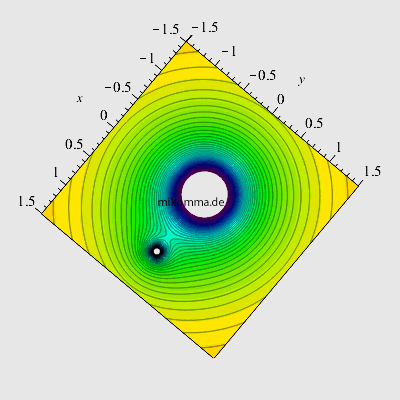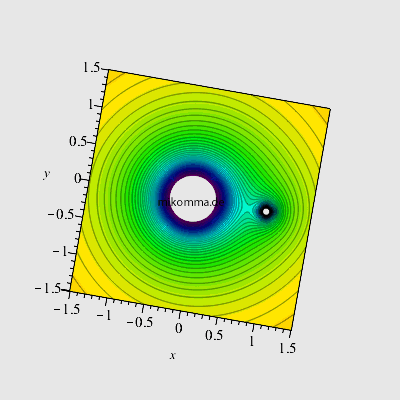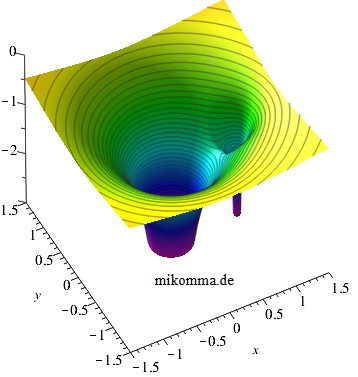
Angenommen zwei Massen (z.B. Sonne und Erde) sind auf zwei Punkte fixiert (auf dem Papier oder dem Bildschirm :-). Dann gehört zu jeder Masse ein Potentialtrichter, der zur Masse proportional und zum Abstand umgekehrt proportional ist (in der Darstellung sind die Trichter nach unten abgeschnitten, fiktives Massenverhältnis 10:1). Zwischen den beiden Massen liegt ein Sattelpunkt: eine dritte dort ruhende Masse befindet sich im labilen Gleichgewicht (in x-Richtung) und "stürzt" bei der geringsten Störung in einen der beiden Trichter.

Natürlich kann man zwei Massen nur auf dem Papier auf zwei Punkte fixieren. In der Realität ziehen sich zwei Massen an und würden sich (aus der Ruhe startend) beschleunigt geradlinig aufeinander zu bewegen und kollidieren. Dass die Erde nicht in die Sonne fällt, liegt daran, dass sich beide Massen um ihren gemeinsamen Schwerpunkt bewegen. Kepler hat die Lösung für dieses Zweikörperproblem angebahnt, und seit Newton haben wir die Bewegungsgleichungen dafür (die sich für zwei Körper geschlossen/analytisch lösen lassen).

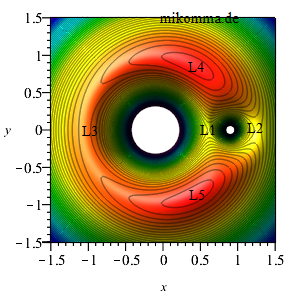
Anscheinend kommt es auf das Bezugssystem an: Die Animation zeigt die Bewegung der beiden Massen in einem Inertialsystem, z.B. dem System der Fixsterne oder siderisch. Im Bezugssystem der Erde (synodisch) ruhen die Potentialtrichter, aber dieses System ist kein Inertialsystem, sondern...:

Im rotierenden System (z.B. Erde - Sonne) kommt zu dem Gravitationspotential das Zentrifugalpotential hinzu, das quadratisch mit dem Abstand zum gemeinsamen Schwerpunkt zunimmt. Dadurch verschiebt sich der Sattelpunkt von oben etwas (L1). Außerdem entstehen zwei weitere Sattelpunkte auf der Verbindungslinie Sonne - Erde, nämlich die Lagrangepunkte L2 und L3 (L1, L2, L3 werden die 'kollinearen L-Punkte' genannt), sowie die L-Punkte L4 und L5 als Maxima des resultierenden Potentials (rote Berggipfel), die mit den beiden Massen gleichseitige Dreiecke bilden. In allen L-Punkten ist eine dritte im rotierenden System ruhende Masse im labilen Gleichgewicht. Dennoch gibt es stabile Bahnen um diese Librationspunkte, weil die Corioliskraft eine Ablenkung bewirkt, die proportional zur Geschwindigkeit der dritten Masse ist. Diese 'rollt also nicht einfach den Berg hinunter', sondern wird um so stärker (nach rechts) abgelenkt, je schneller sie sich bewegt, 'steigt also wieder aufwärts' - wenn die Anfangsbedingungen stimmen.
Und wir werden noch sehen, dass es nicht ganz einfach ist, die passenden Anfangsbedingungen zu finden...

Bevor wir die Bewegungsgleichungen aufstellen noch eine Bemerkung zu den gängigen Konventionen: Es ist üblich (weil zweckmäßig), die Gesamtmasse M(Sonne) + m(Erde) = 1 zu setzen, und als Ursprung des synodischen Systems den gemeinsamen Schwerpunkt zu wählen. Dann ist der Abstand zwischen M und m gleich 1 und M befindet sich bei x = -m, und m bei x = 1-m (die x-y-Ebene ist 'die Ekliptik'). Wählt man noch die Gravitationskonstante gleich 1, so rotiert das synodische System mit der Winkelgeschwindigkeit 1 und man erhält als Bewegungsgleichungen für einen dritten Körper im synodischen System, dessen Masse im Vergleich zu M und m vernachlässigbar ist:

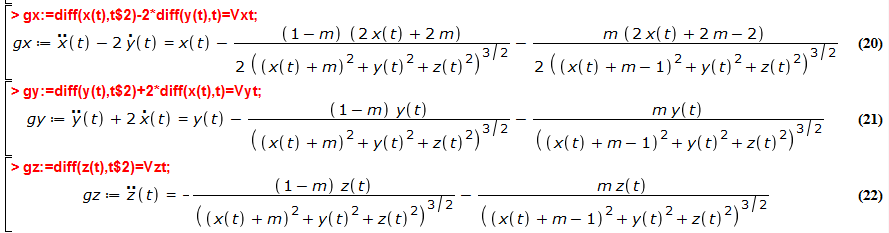
Dabei steht auf den rechten Seiten der Gleichungen jeweils die partielle Ableitung des Potentials nach der entsprechenden Koordinate. Nun ja - das sieht nicht gut aus: die Gleichungen sind nicht nur gekoppelt, sondern auch noch ('hochgradig') nichtlinear und lassen sich nicht analytisch lösen, das Dreikörperproblem eben. Um eine Ahnung davon zu bekommen, wie sich der dritte Körper 'im Prinzip' in der Nähe der Librationspunkte bewegt, kann man die Gleichungen linearisieren, also eine Reihenentwicklung der rechten Seiten um L1...L5 machen. Dann entkoppelt die Gleichung für z(t) und wird zu einer 'normalen Schwingungsgleichung'. Für die Bewegung in x- und y-Richtung (in der Ekliptik) findet man ebenfalls Schwingungsgleichungen (mit anderer Frequenz), aber 'leider' auch exponentielle Anteile (als Funktion der Zeit). Exponentielle Anteile mit negativem Exponenten sind dabei nicht kritisch, weil sie von selbst abklingen (gedämpfte Schwingung). Aber positive Exponenten befördern die dritte Masse 'ziemlich schnell ins Jenseits', falls man nicht durch 'geeignete Anfangsbedingungen' dafür sorgt, dass die Amplitude dieses Terms möglichst klein ist, am besten gleich 0. Das lässt sich erreichen, und man hat damit eine erste Näherung bzw. eine erste Antwort auf die Frage, wie man einen Satelliten in den L-Punkten stationieren kann. Umgekehrt kann man natürlich den positiven Exponenten (a*t, a>0) negativ machen, indem man die Zeit rückwärts laufen lässt. Dann fliegt der Satellit nicht 'exponentiell weg', sondern landet sanft in einer 'labilen Librationsbahn'. Und genau dies wird verwendet, wenn man Satelliten in L1 bis L3 'parken' will.

Kollineare L-Punkte

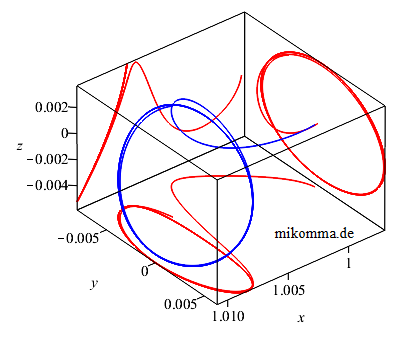
Die Sattelpunkte sind grundsätzlich instabil, d.h., ein Satellit kann sich dort nicht beliebig lange halten, sondern muss durch Steuermanöver kontrolliert werden.
Nebenstehend ist exemplarisch eine Bahn um den L2 gezeigt, die von der Erde aus (rechts, etwas außerhalb des Bildes, synodisches Bezugssystem) erreicht werden kann. Die blaue Kurve zeigt die 3D-Bahn, die roten Kurven sind die Projektionen auf die Koordinatenebenen. Die (fast) geschlossene Bahn besteht aus acht Umläufen, die jeweils etwa ein halbes Jahr dauern (man muss also nicht allzu oft nachsteuern). Für den Einschuss in die Bahn (seine Darstellung) wurde einfach die Berechnung ein (knappes) halbes Jahr früher gestartet. Umgekehrt würde sich der Satellit aus der geschlossenen Bahn schnell verabschieden, wenn man ein halbes Jahr zu lang wartet. Bei der gezeigten Bahn handelt es sich um eine 'Halo-Bahn', die ihren Namen von dem Aussehen der Projektion auf die y-z-Ebene hat, also von der Erde aus gesehen so erscheint. Halo-Bahnen entstehen, wenn die Frequenzen der Schwingungen in z-Richtung und in x-y-Richtung nahezu gleich sind. Liegt die Bahn in der Ekliptik, so spricht man von Ljapunov-Bahnen, die dann so aussehen, wie die gezeigte Projektion auf die x-y-Ebene (aber für die Raumfahrt nicht besonders interessant sind).

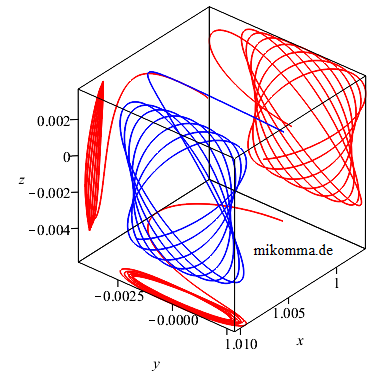
Die Frequenzen der Schwingungen in z-Richtung und in x-y-Richtung sind nur für (relativ) große Amplituden nahezu gleich. Verkleinert man den Abstand zum L-Punkt, so unterscheiden sie sich merklich, und man erhält Lissajous-Bahnen. Alles klar?

Anmerkungen zur Methode: Die Bewegungsgleichungen wurden mit Maple numerisch integriert. Es empfiehlt sich eine Rechengenauigkeit von mindestens 30 geltenden Ziffern, weil sich sonst alleine durch das 'numerische Rauschen' der Satellit aus der instabilen Ruhelage entfernt (Ljapunov lässt grüßen!).
'Geeignete Anfangsbedingungen' findet man mit einem 'first guess' mithilfe der linearisierten Bewegungsgleichungen etwa auf 3 geltende Ziffern genau. Für jeden weiteren 'geschlossenen Umlauf' muss man dann die Anfangsbedingungen um etwa 3 geltende Ziffern verfeinern (Ljapunov lässt noch einmal grüßen!).

Im Vergleich zu den kollinearen L-Punkten sind L4 und L5 nicht nur für den Maple-Programmierer, der sich nach mehr oder weniger stabilen Bahnen sehnt, ein gefundenes Fressen:

Trojaner

Im Gegensatz zu L1...L3, die 'selbstreinigend' sind, weil sich dort kein Körper lange ohne Nachsteuerung aufhalten kann, sind L4 und L5 aus der Sicht des (Maple-) Programmierers 'pflegeleicht', weil dort nicht schon nach der kleinsten Störung das Chaos ausbricht. Vielmehr kann dort 'der dritte Körper' (oder Mann?) beliebig lange auf den Bergrücken des Potentials hin und her wandern. Die Corioliskraft bewahrt ihn vor dem Abgleiten. 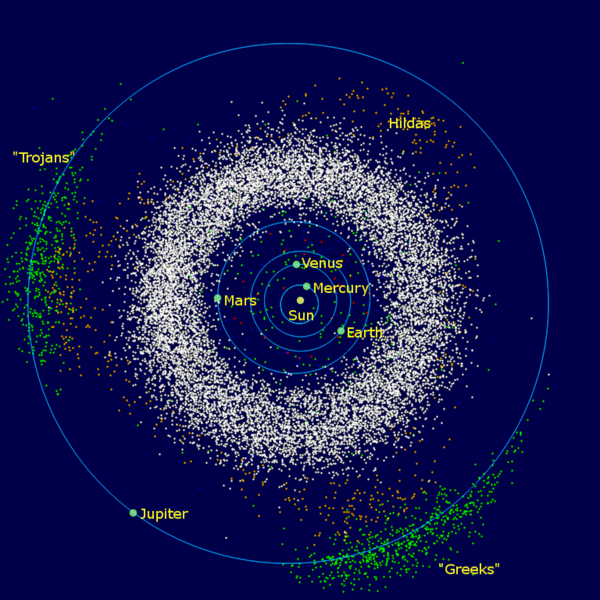Dabei ergeben sich Zykloidenbahnen, wie bei der Bewegung von Elektron in gekreuzten Feldern. Aus diesem Grund sammelten sich z.B. im System Sonne - Jupiter Trojaner an,
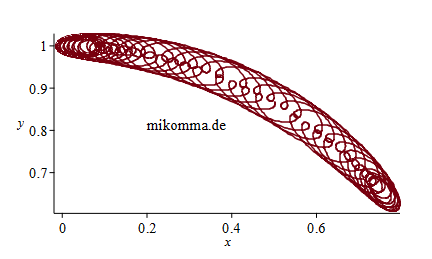die je nach 'Anfangsbedingung' weite Reisen machen (Bild oben) oder praktisch ortsfest bleiben (Bild rechts, Maßstab beachten). Übrigens...: Die Fragestellung wie man einen Körper auf einem Sattel balanciert gibt es auch in der Teilchenphysik. Wenn der Sattel mit der passenden Frequenz rotiert, kann man Herrn Ljapunov einen Streich spielen und bekommt beliebige Kombinationen aus Halo- und Lissajous-Orbits in einer Paulfalle. Es ist schon erstaunlich, dass sich die Natur immer an die gleichen 'Gesetze' hält - egal in welcher Größenordnung. Woran das wohl liegt?
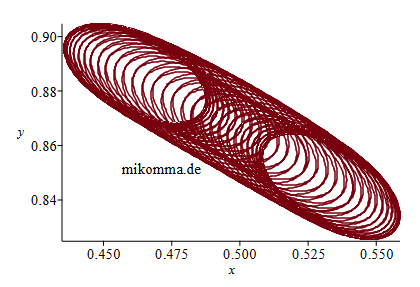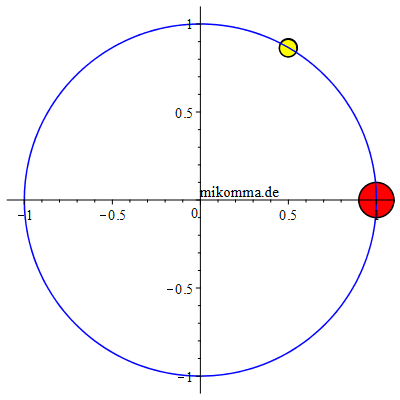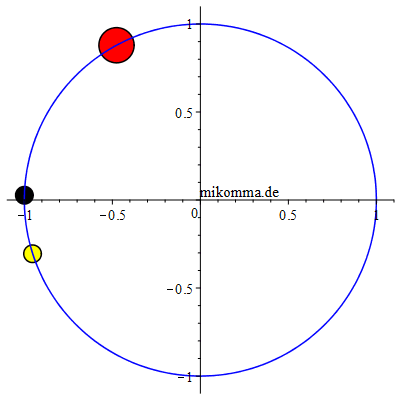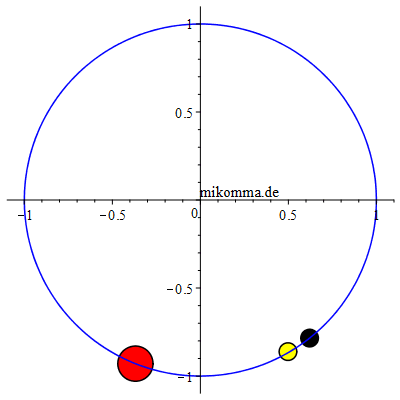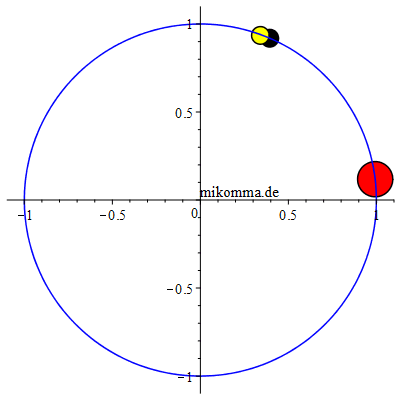
Die Trojanerbahnen von oben in gleichem Maßstab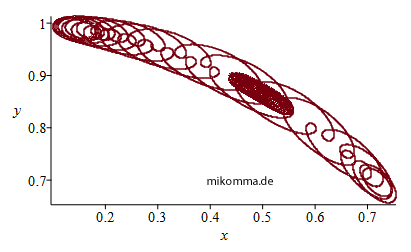 Rechts: "Jupiter (großer roter Fleck) auf der Jagd nach einem Trojaner" (gelb) im Inertialsystem (siderisch). Jupiter - zur Vereinfachung auf eine Kreisbahn gesetzt -, L4 (schwarz) und die Sonne (im Ursprung gedacht) bilden immer ein gleichseitiges Dreieck. Wenn man alle 410 Bilder abwartet, sieht man die Wanderung des Trojaners auf der "langen Bahn" (siehe oben), beginnend in L4 und (fast) wieder endend in L4. Und wenn man genau hinschaut, sieht man auch die 'Übersetzung' der Zykloidenbahnen vom synodischen System ins siderische: azimutal pendelt der Trojaner bezüglich L4 in Schüben 'vorwärts' und dann wieder 'rückwärts', wobei er auch radial zwischen 'Außenbahn und Innenbahn' pendelt.

Sie vermissen die stabile Mannigfaltigkeit? Da muss ich Sie leider mit R.P.F. vertrösten: "It is so complicated, that we postpone this problem until next year."

Links

'Moderne Physik mit Maple'