|
SIR-Modell in Corona-Zeiten In diesem Artikel wird ein alt bekanntes und stark vereinfachtes Modell vorgestellt, mit dem man qualitativ beurteilen kann, welche Größen eine Epidemie bestimmen, und wie man u.U. den Verlauf der Epidemie beeinflussen kann. Das SIR-Modell Man teilt zunächst die Population in drei Klassen: S = Susceptibles: Anfällige, die infiziert werden können, I = Infectives: Angesteckte, die infizieren können, R = Recovered: Geheilt (immun = Resistant), bzw. Removed (= immun oder gestorben).
Das System der Differentialgleichungen lautet
Diese nichtlineare DGL koppelt S und I: Die Abnahme der Suszeptiblen ist proportional (k1 = Infektionsrate) zum Produkt der Suszeptiblen und Infizierten.
Die Zahl der Infizierten erhöht sich im gleichen Maß wie sich S verringert (erster Summand), und nimmt mit der Gesundungsrate k2 ab (zweiter Summand, linearer Zusammenhang). Weil k2 auch I an R koppelt (s.u.), ist die Gl. 2 wichtig für das Verständnis der Dynamik des Systems: Die Zahl der Infizierten nimmt für die Differenz D = k1*S - k2 > 0 exponentiell zu, für D = 0 bleibt sie konstant und für D < 0 nimmt sie exponentiell ab. Wenn man die Strategie verfolgt, D immer knapp unter 0 zu halten, ist das Risiko eines erneuten exponentiellen Wachstums (Ausbruchs) von I sehr hoch, solange I sehr klein ist:
Die Klasse R nimmt mit der "Gesundungsrate" k2 proportional zu I zu. Erst für große I nimmt R merklich zu und man erreicht in endlicher Zeit "Herdenimmunität". Rechnet man in Einheiten der Gesamtpopulation, so lautet die Nebenbedingung
bzw. die Größen S, I, und R sind prozentuale Angaben. Anm.: Zur Umrechnung auf absolute Größen muss I(t) neu skaliert werden und die hier dargestellten Kurven für I(t) wären dann im Verhältnis zu S(t) und R(t) wesentlich niedriger. Es geht aber in diesem Beitrag mehr um prinzipielle Aussagen, also den Verlauf der Kurven, und nicht um absolute Größen. Anmerkungen zum exponentiellen Wachstum, Begriffsklärungen: Die Exponentialfunktion y = bt ist für die Basen b für b = 0.1 bis b = 2.0 in Schritten von 0.1 dargestellt (rot: b>1, schwarz: b=1, blau: b<1, Zeit t in Einheiten einer Generation, z.B. 4 Tage):
Für b<1 handelt es sich um einen exponentiellen
Zerfall, für b=1 bleibt die Funktion (die Zahl der Infizierten) konstant, und
für b>1 wächst die Funktion exponentiell (was im rechten Schaubild verdeutlicht
wird). Übrigens (04.06.20). Ein Tourismusminister sagte (sinngemäß): "Nachdem nun der R-Faktor stabil kleiner Null ist, können wir wieder lockern". Was bedeutet R < 0? Einer steckt weniger als keinen an? Also rein mathematisch geht das schon:
Für negative Basen b (oder R) wird die Exponentialfunktion komplex: Realteil rot, Imaginärteil blau, Betrag grün. Spaß beiseite, jetzt wird es ernst:
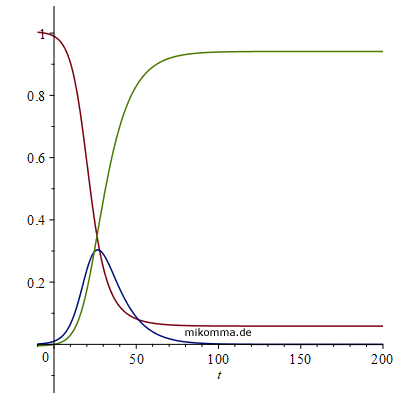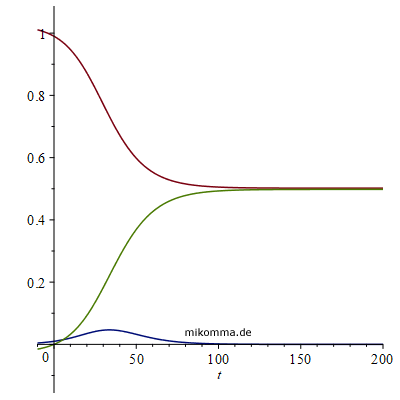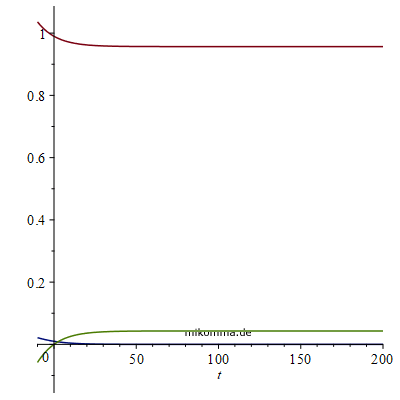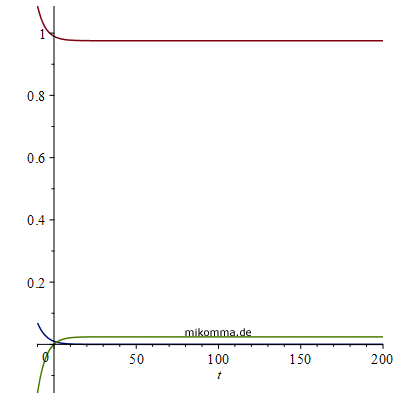
Die Rolle der Parameter und Anfangsbedingungen Ohne Maßnahmen ("wenn man der Natur ihren freien Lauf lässt") sieht der Verlauf der Epidemie in Abhängigkeit von den Parametern und Anfangsbedingungen etwa so aus (S=rot, I=blau, R=grün, Animationen im Sekundentakt). Änderung der Infektionsrate k1 von 0.1 bis 0.5, k2=0.1, I(0)=0.01, R(0)=0
Je höher die Infektionsrate, desto höher das Maximum der Infizierten, das dann um so früher erreicht wird. Man beachte auch die Werte von S und R für große Zeiten (asymptotisch, Herdenimmunität). Änderung der Gesundungsrate k2 von 0.1 bis 0.5, k1=0.3, I(0)=0.01, R(0)=0
Der Zeitpunkt des Infektionspeaks ändert sich für k2 < k1 nur wenig (tritt mit wachsendem k2 etwas später ein). Für k2 > k1 klingt I(t) exponentiell ab, d.h., es entsteht keine Epidemie. Änderung von I(0) von 0.001 bis 0.01, k1=0.3, k2=0.1, R(0)=0
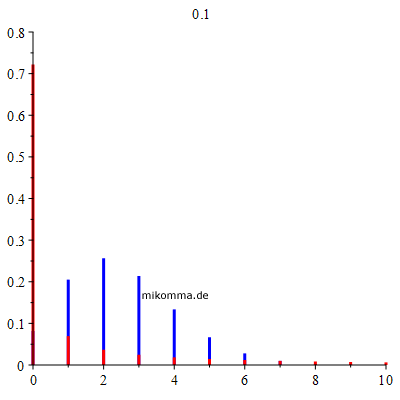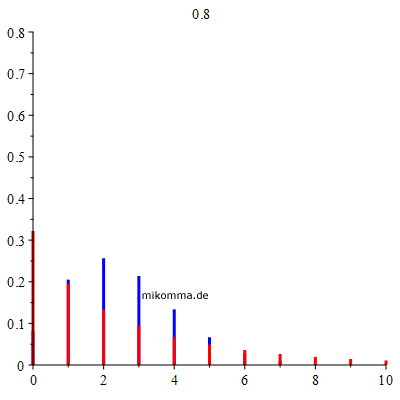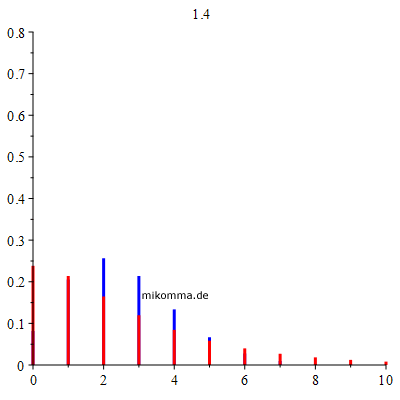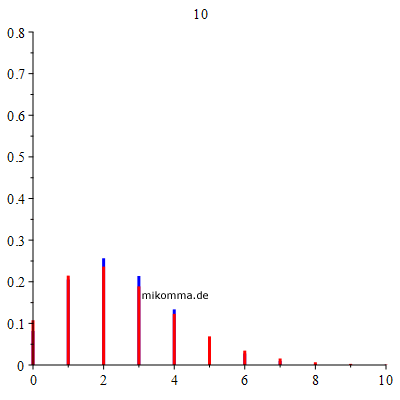
Die Änderung des Anteils der anfänglich Infizierten I(0) ist praktisch gleichwertig mit einer Verschiebung des zeitlichen Verlaufs von S, I und R. Das ist ein typisches Merkmal dieser Art Epidemie: Es ist nicht eine Frage ob sie ausbricht, sondern nur wann sie (wieder) ausbricht. Das "Austreten einzelner Feuerherde" oder die "Unterbrechung von Infektionsketten" reicht nicht aus, so lange die Herdenimmunität nicht errreicht ist. Es gibt kein "vor dem exponentiellem Wachstum", weil das exponentielle Wachstum schon mit dem ersten Infizierten beginnt. Ergänzung (04.06.20): Der sogenannte "Dispersionsfaktor k" bezieht sich auf sogenannte "Superspreader". Wenn k sehr klein ist, bedeutet das im Rahmen des SIR-Modells, dass sich die Zahl der Infizierten sprunghaft ändern kann, also obige Kurven nach vorne (zu kleineren Zeiten) verschoben werden, was z.B. geschehen kann, wenn (nur) ein Infizierter zusammen mit vielen nicht Infizierten in einem geschlossenen Raum laut singt. Genauer gesagt: Die Reproduktionszahl R ist ein Mittelwert einer Wahrscheinlichkeitsverteilung. Wenn es sich um "seltene Ereignisse" handelt, geht man in der Regel von einer Poissonverteilung (P) aus. Wenn die Ereignisse "noch seltener" sind, geht man zur "negativen Binomialverteilung" (NB) über. Die nachfolgende Animation zeigt beide Verteilungen im Vergleich.
NB = rot, P = blau für einen Mittelwert R = 2.5 (bitte Skalierung der Achsen beachten). Der Dispersionsparameter wird oben angezeigt, das erste Bild für zehn Sekunden, dann im Sekundentakt. Die wesentliche Aussage in diesem Zusammenhang ist: Man sollte nicht nur mit Mittelwerten rechnen. Siehe auch: Estimating the overdispersion in COVID-19 transmission using outbreak sizes outside China.
Änderung von R(0) von 0.07 bis 0.7, k1=0.3, k2=0.1, I(0)=0.01.
Wenn zu Beginn der Ausbreitung der Epidemie schon 66% der Population immun wären, wäre das Maximum der Infizierten = I(0): Herdenimmunität. Maßnahmen Bis hierher haben wir "der Natur ihren freien Lauf gelassen". Lässt sich der Verlauf der Epidemie auch beeinflussen? Wenn es keinen Impfstoff und keine Medikamente gibt, bleibt nur eine Reduzierung der Infektionsrate k1, bzw. eine Reduzierung von k1*S(t)*I(t). Das geht nur über eine Verringerung der S-I-Kontakte. Hier ist ein Beispiel, in dem in den SIR-Gleichungen die Infektionsrate mit einer Amplitude Amp multipliziert wird, mit dem Ziel, den Anteil der Infizierten nicht über 10% (also 8Mio in der BRD) steigen zu lassen.
Zu Beginn ist der Anteil der Infizierten I(0)=0.001. Nach 20 Tagen wird für 30 Tage die Infektionsrate auf 10% reduziert (90% Kontaktsperre). Dann ist I(50)=0.006 und nach einer Aufhebung der Kontaktsperre I(70)=12%. Nach einer erneuten Kontaktsperre von 30 Tagen ist I(100)=1% und R(100)=30%. Deshalb scheint es auszureichen, für weitere 100 Tage die Kontakte um 20% zu reduzieren, damit die Epidemie "beherrschbar bleibt". Bezogen auf Covid 19 ist dieses Beispiel aber wohl zu optimistisch, bzw. das Problem mit dem exponentiellen Wachstum ist, dass es mit dem ersten Infizierten beginnt, aber meistens erst bemerkt wird, wenn es zu spät ist. In obiger Simulation wurden die Kontakte in der "letzten Phase" auf 80% beschränkt. Was wäre wenn man stattdessen eine Impfung zur Verfügung hätte?
Das Imperial College COVID-19 Response Team schlägt in seinem "Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand" vom 16.03.20 ein "adaptives Triggern" vor, d.h., wenn die Zahl der Infizierten (genauer die Zahl der ICU cases) eine bestimmte Schwelle übersteigt, wird die Infektionsrate durch Kontaktsperren reduziert (schlagartig wie in obigem Beispiel), und wenn eine zweite bestimmte Schwelle unterschritten wird, wird die Kontaktsperre wieder aufgehoben. Das adaptive vorgehen ist natürlich sinnvoll, nur weiß man derzeit noch nicht genau, wo diese Schwellen liegen "fährt also auf Sicht". Aber man kann für eine erste Orientierung die Infektionsrate auch cosinusförmig modulieren (von 1 = "Normalbetrieb" bis 0 = "alle zu Hause" und wieder zurück). Auch wenn das nicht umsetzbar ist, kann man der folgenden Animation doch einiges entnehmen. Die Periode in Tagen wird oben angezeigt, die schwarze Cosinuskurve visualisiert nur die Periode und nicht die Amplitude. Für große Perioden kann man auch an saisonale Schwankungen denken:
Welche Variante bevorzugen Sie? Oktober 2020: Neueste Erkenntnis der Verantwortlichen zur Inzidenzzahl. "Wir sind mitten in der zweiten Welle":
Wenn es 3,5 Zeiteinheiten (z.B. Wochen) dauert, bis die Inzidenzzahl von 1 auf 35 steigt, dann dauert es nur noch eine knappe halbe Woche, bis die 50 erreicht ist. Man sollte also "Alarmstufe rot" ausgelöst haben, wenn die Inzidenzzahl in zwei Wochen von 1 auf 7 gestiegen ist (weil sie dann nach weiteren 2 Wochen bei 50 ist). Zahlen, die bei Verhandlungen "gegriffen" werden, orientieren sich nun mal am linearen Wachstum (und den Interessen der Verhandler), und dann gibt man sich erstaunt, dass die Werte auf einmal "explodieren". © März 2020, Dr. Michael Komma (VGWORT) Links: Die mathematische Beschreibung dynamischer Systeme verwendet Systeme von Differentialgleichungen, die eng verwandt sind mit der Beschreibung atomarer Übergänge (Systeme mit zwei Zuständen), siehe z.B. Spontane Emission | Kaskade | Photogalerie | Photonenemission | Weisskopf-Wigner
HOME | Fächer | Physik | Elektrizität | Optik | Atomphysik | Quantenphysik | Top |







![Typesetting:-mprintslash([Amp := PIECEWISE([1, `<`(t, 20)], [.1, `<`(t, 50)], [1, `<`(t, 70)], [.1, `<`(t, 100)], [.8, otherwise])], [piecewise(`<`(t, 20), 1, `<`(t, 50), .1, `<`(t, 70), 1, `<`(t, 100...](images/sirpub_17.gif)




 oder
1:1
oder
1:1 