Zum Kreispendel sagt man manchmal auch "ebenes mathematisches Pendel" und meint damit eine punktförmige Masse, die sich reibungsfrei auf einem Kreis bewegt, der im Schwerefeld "senkrecht steht". Manchmal ist damit auch ein Fadenpendel gemeint, dessen punktförmige Masse sich auf einem horizontalen Kreis bewegt (wozu man meistens "Kegelpendel" sagt).

Die Differentialgleichung des hier behandelten Kreispendels lautet 

(1)

und ist leider nur numerisch lösbar. Das nächste Diagramm zeigt den Winkel, die Winkelgeschwindigkeit und die Winkelbeschleunigung als Funktionen der Zeit, wenn die Geschwindigkeit im tiefsten Punkt "gerade ausreicht" um über den oberen Totpunkt zu kommen:  

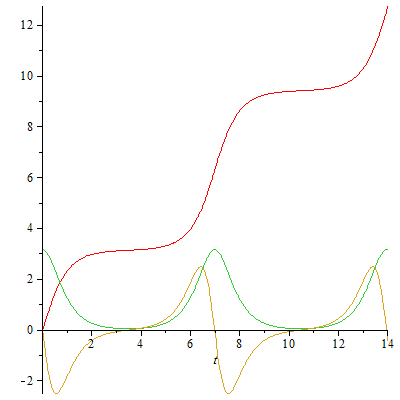Wenn das Pendel genau mit der Geschwindigkeit startet, die erforderlich ist, um den oberen Totpunkt zu erreichen, kommt es genau genommen nie oben an (aperiodischer Grenzfall, gesättigtes Wachstum). Eine Horrorvorstellung für jeden Überschlagsschaukler! Aber keine Sorge, meines Wissens wurde bis heute diese "exakte Lösung" nicht realisiert, nicht einmal auf meinem Computer! Es genügt schon ein minimales "numerisches Rauschen" (etwa 10 Stellen hinter dem Komma :-) um die Bewegung in endlicher Zeit ablaufen zu lassen.

Aber bitte mit Pfeilen!
Grün: Geschwindigkeit, blau: Zentripetalbeschleunigung, rot: Gesamtbeschleunigung = Zentripetalbeschleunigung + Tangentialkomponente der Schwerebeschleunigung. (Die Normalkomponente der Schwerkraft wird durch die Führungskraft kompensiert.)

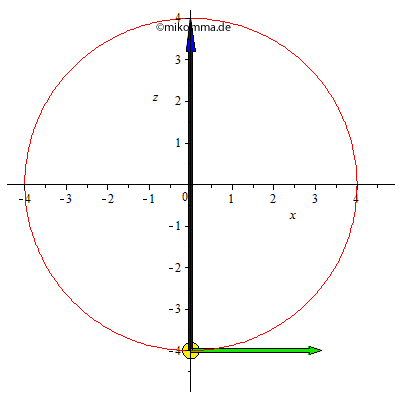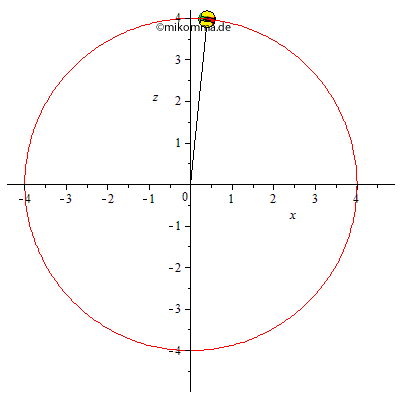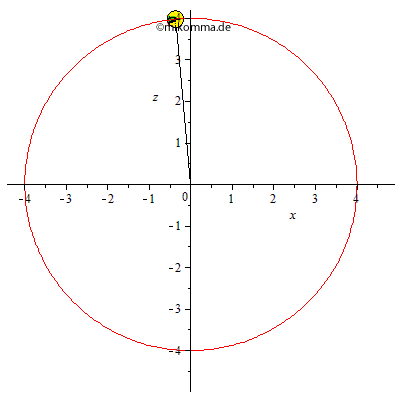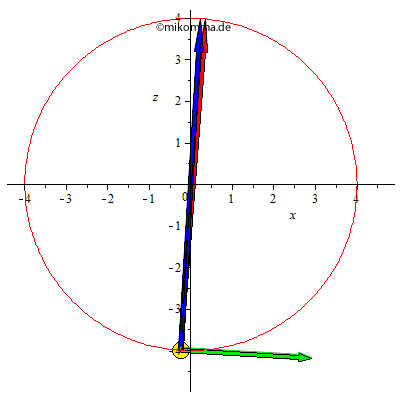
"Technische Anmerkung" (2011): In der Nähe des oberen Totpunktes wackelt eventuell die Gerade (vom Ursprung/Zentrum zum Pendelkörper). Es ist eben nicht ganz einfach, eine fast senkrechte Gerade auf den Bildschirm zu bringen. Beim Export von MAPLE nach GIF (und nachfolgender Kompression) wird außerdem das Antialiasing abgeschaltet. Und dann reagiert noch der eine Browser so und der andere so. Oder wie wäre es mit einer neuen Graphikkarte?

Eine beliebte (zumindest bei Lehrern :) Physikaufgabe lautet: Aus welcher Höhe muss eine Loopingbahn mindestens starten, damit nicht angeschnallte Fahrgäste nicht herausfallen? Wir ergänzen: Wie würde die Flugbahn von nicht befestigten Gegenständen bei verschiedenen Starthöhen aussehen (die DGL (1) wird nicht benötigt)?

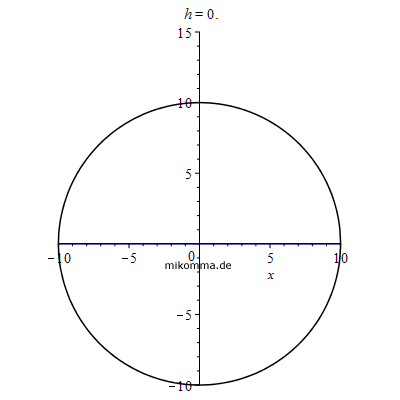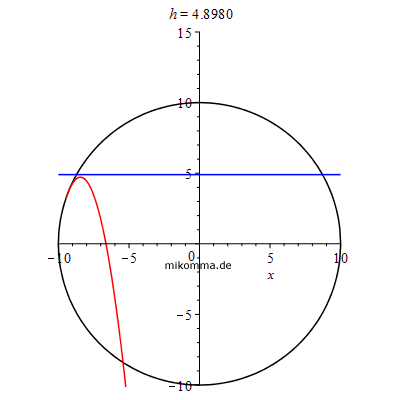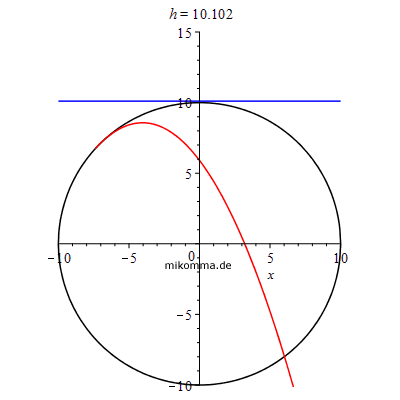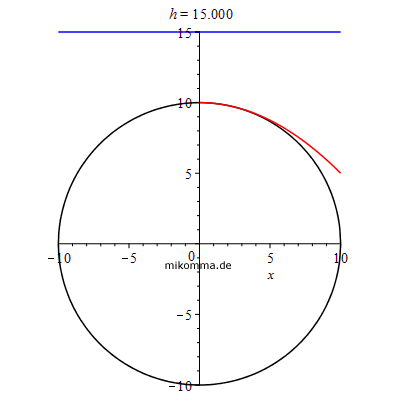Man denke sich eine Anlaufbahn, die unten im Kreis von rechts in den Looping führt (z.B. ein Hemmungspendel). Die Starthöhe h wird vom Mittelpunkt des Kreises nach oben gezählt und ist als blaue Linie dargestellt.

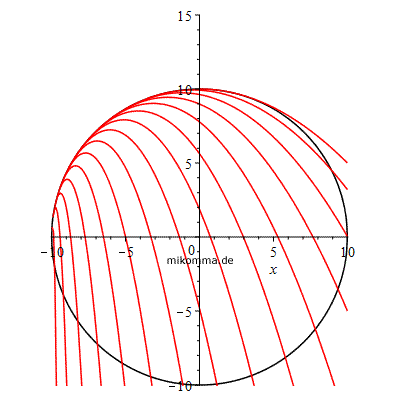Parabelschar für die Starthöhen 1 bis 15. Die nächste beliebte Physikaufgabe könnte z.B. lauten: Bei welcher Starthöhe entsteht beim Auftreffen auf die Kreisbahn der größte Schaden?