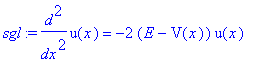

Ein Wellenpaket in die SGL einsetzen...
| > | restart: |
| > | sgl:=diff(u(x),x$2)=-2*(E-V(x))*u(x); |
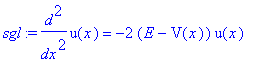
Wellenpaket (Normierung sqrt(Pi)):
| > | gp:=exp(-x^2/2); |
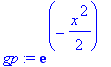
| > | subs(u(x)=gp,sgl); |
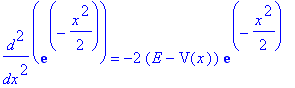
| > | simplify(%); |

| > | expand(%/2/gp); |

Für ein quadratisches Potential ist also das Gaußpaket zur Energie E = 1/2 eine Lösung der stationären SGL. Man kann das Wellenpaket "anhalten"!
| > | V:=x->x^2/2; |
![]()
Operatoren
Für den harmonischen Oszillator (quadratisches Potential) lässt sich die SGL auch so schreiben:
| > | (x^2*u(x)-diff(u(x),x$2))/2-E*u(x)=0; |

Das erinnert die dritte binomische Formel - hier allerdings für Operatoren
| > | dop:=Diff(``,x): dop2:=Diff(``,x$2): |
| > |
| > | x^2-dop2=(x+dop)*(x-dop); |

| > |
| > | Op:=u->((x*u+diff(u,x))/sqrt(2)); |

| > | Ops:=u->(x*u-diff(u,x))/sqrt(2); |

| > |
Anwendung des Operators
| > | simplify((Ops@Op)(u(x))); |
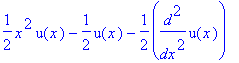
Das ist die linke Seite der Schrödingergleichung zur Energie 1/2.
| > | simplify((Op@Ops)(u(x))); |

Das ist etwas anderes, es kommt also auf die Reihenfolge der Anwendung der Operatoren an und es gilt:
| > | %-%%; |
![]()
Der Kommutator der beiden Operatoren ist also der Einheitsoperator
| > |
Was machen die Operatoren aus dem Paket?
| > | (Op@Ops)(gp); |

Der Grundzustand bleibt erhalten
| > | (Ops@Op)(gp); |
![]()
oder wird vernichtet. Wie funktioniert das?
| > | Ops(gp); |

Eine neue Funktion? Und wieder zurück:
| > | Op(%); |

| > |
| > | subs(u(x)=Ops(gp),sgl); |

| > | simplify(%); |
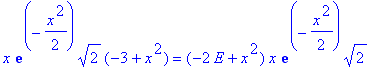
| > | expand(%/gp/sqrt(2)); |
![]()
| > |
Das stimmt für E = 3/2! Ops erzeugt also aus dem Grundzustand eine neue Lösung. Wir vergleichen mit den bekannten Lösungen (ohne sqrt(Pi)):
| > |
| > | v:=(n,x)->1/sqrt(2^n*n!)*HermiteH(n,x)*exp(-x^2/2); #*Pi^(-1/4); |

| > | simplify(v(1,x)); |

| > | Ops(gp); |

| > |
| > | simplify((Ops@@3)(gp)); |

| > | simplify(v(3,x)); |

| > | #int(gp^2,x=-infinity..infinity); |
| > | seq(int((Ops@@n)(gp)^2,x=-infinity..infinity),n=1..5); |
![]()
Zur Normierung fehlt also nur der Faktor
| > | 1/sqrt(n!)/Pi^(1/4); |
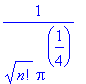
Wir verzichten wieder auf sqrt(Pi)
| > |
| > | erz:=(u,n)->(Ops@@n)(u)/sqrt(n!); |

| > | test:=simplify(erz(gp,6)); |

| > |
| > | simplify(v(6,x)); |

| > |
| > | vern:=(u,n)->(Op@@n)(u)/sqrt(n!); |

| > | simplify(vern(test,6)); |

| > |
Leiteroperatoren mit Normierung
| > | auf:=(u,n)->Ops(u)/sqrt(n+1); |
![]()
| > | auf(test,6); |

| > | simplify(%); |
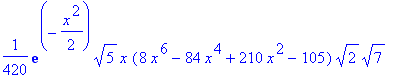
| > |
| > | ab:=(u,n)->Op(u)/sqrt(n); |
![]()
| > | simplify(ab(test,6)); |

| > | #simplify(v(5,x)); |
| > |
Reihenansatz
| > | restart: |
| > | with(powseries): |
| > | sgl:=diff(psi(x),x$2)+2*(E-x^2/2)*psi(x)=0; |

Mit powsolve(DGL)
| > | sol:=powsolve(sgl); |
![]()
wird die DGL mit einem Reihenansatz (formale Reihe) gelöst:
| > | tpsform(sol,x,7); |

![]()
C0 und C1 sind die Werte für Anfangsbedingungen psi(0) und D(psi)(0).
| > |
Koeffizienten a(_k) der Reihe
| > | sol(_k); |
![]()
Die Reihe sollte abbrechen. Für welches E?
| > | solve(sol(_k),E); |
![]()
Die Rekursion stört. Wir versuchen es mit einer Reihe, die schon das GP enthält:
| > |
| > | psi:=x->exp(-x^2/2)*f(x); |

| > | powsolve(sgl) ; |
Error, (in spcldif) final value in for loop must be numeric or character
| > | sgl; |

| > | # muss erst vereinfacht werden |
| > |
DGL für f(x)
| > | sgls:=simplify(simplify(factor(sgl))*exp(x^2/2)); |

| > | sols := powsolve(sgls) : |
| > | sols(_k); |
![]()
Verschiebung des Index
| > | subs(_k=n+2,%); |
![]()
Eigenwerte
| > | solve(%,E); |
![]()
| > | f7:=tpsform(sols,x,8); |
![]()
![]()
| > | subs(E=7+1/2,f7); |
![]()
| > | simplify(HermiteH(7,x)*3/7!); |
![]()
Scheint zu passen...
| > | #v:=(n,x)->1/sqrt(2^n*n!)*HermiteH(n,x)*exp(-x^2/2); #*Pi^(-1/4); |
| > | #simplify(v(7,x)); |
Und hier ist die Prozedur:
| > | restart: |
| > | psi:=proc(n,x) local sgls,sols,f,u,N; sgls := -f(x)-2*diff(f(x),x)*x+diff(f(x),`$`(x,2))+2*f(x)*E = 0; sols := powseries[powsolve](sgls) : f:=convert(powseries[tpsform](sols,x,n+1),polynom); f:=subs(C0=Re(I^n),C1=Im(I^n),E=n+1/2,f); u:=exp(-x^2/2)*f; N:=int(u^2,x=-infinity..infinity); u/sqrt(N); end; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > |
| > | psi(7,x); |

| > | #v:=(n,x)->1/sqrt(2^n*n!)*HermiteH(n,x)*exp(-x^2/2)*Pi^(-1/4): |
| > | #simplify(v(7,x)); |
| > |
| > | plot(psi(7,x),x=-6..6); |
![[Maple Plot]](images/harmoszop65.gif)
| > |
| > | plot(psi(8,x)^2,x=-6..6); |
![[Maple Plot]](images/harmoszop66.gif)
komma@oe.uni-tuebingen.de