Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel 4.1.2
Worksheet wirf2_10.mws
c International Thomson Publishing Bonn 1995 filename: wirf2.ms
Autor: Komma Datum:28.3.94
Thema: Schwache Extrema
Als Lösung der Wurfbewegung wird ein Polynom 3.Grades
vorgegeben dessen Formvariablen variiert werden. Das schwache
Minimum wird exakt berechnet und im Parameterraum dargestellt.
| > |
Im vorangehenden Beispiel (wirf1a.ms) wurde für x(t) bewußt eine "falsche" Funktion verwendet, um einen ersten Einblick zu bekommen, wie die Wirkung darauf reagiert. Der Ansatz einer virtuellen Bahn, die aus stückweise gleichförmigen Bewegungen besteht, führt letzten Endes auf die Feynmanschen Pfadintegrale, wenn man alle möglichen Bahnen berücksichtigt, also unendlich viele Zwischenpunkte zuläßt. Damit erfaßt man dann auch alle Funktionen, von denen am Schluß nur die "richtige" übrigbleiben sollte. Die Variationsrechnung löst dieses Problem geschlossen mit den Euler-Lagrange Gleichungen. Diese Gleichungen liefern zwar die wirkliche Bahn, aber sie geben keinen Einblick in die Bewertung und die Bedeutung der virtuellen Bahnen. Nachdem aber die Natur zumindest im atomaren Bereich auf diese Bahnen einen ebenso großen Wert zu legen scheint wie auf das Endprodukt, wollen auch wir diesen Weg beschreiten und die Suche nach der minimalen Wirkung an einem weiteren einfachen Beispiel fortsetzten.
Wir wissen, daß die Weg-Zeit-Funktion des senkrechten Wurfes durch eine quadratische Funktion beschrieben wird. Was passiert, wenn wir diesmal nicht wie im vorigen Beispiel (wirf1a.ms) eine lineare Funktion sondern eine kubische Funktion ansetzen? In der Variationsrechnung spricht man von einem schwachen Extremum, wenn man den Funktions*typ* vorgibt. Wie können wir also mit unserem CAS das schwache Minimum finden?
Die Ausgangsgrößen sind sicher wieder die Energien.
| > |
| > | restart; with(plots): |
| > | T:=m/2*v^2: v:=diff(x(t),t): L:=T-V: S:=int(L,t=t0..t1): t0:=0: |
| > |
Die folgende Schleife produziert ein Polynom n-ten Grades. Wir setzen für unsere Zwecke n = 3. Als *exakte* Lösung muß sich dann a2=-1/2g und a3=0 ergeben. Die interessante Frage ist aber, wie die Wirkung für "falsche" Parameter (a[i]) aussieht.
| > | n:=3: |
| > | xx:=proc(t) local xx,i; |
| > | xx:=0; |
| > | for i to n do |
| > | xx:=xx+a[i]*t^i; |
| > | od; |
| > |
| > | RETURN(xx); |
| > | end; |
![]()
| > |
Ein Koeffizient (z.B. a1) läßt sich durch die Bedingung x(t1) = x1 und die anderen Koeffizienten ausdrücken:
| > | as1:=solve(xx(t1)=x1,a[1]); |
![as1 := (-a[2]*t1^2-a[3]*t1^3+x1)/t1](wirf2/wirf2_102.gif)
| > |
Die Weg-Zeit-Funktion und die potentielle Energie lauten dann
| > | x:=t->subs(a[1]=as1,xx(t)); |
![]()
| > | V:=m*g*x(t); |
![V := m*g*((-a[2]*t1^2-a[3]*t1^3+x1)/t1*t+a[2]*t^2+a[3]*t^3)](wirf2/wirf2_104.gif)
| > |
und führen uns zu folgendem Ausdruck für die Wirkung:
| > | S; |
![9/10*m*a[3]^2*t1^5+1/4*(6*m*a[2]*a[3]-m*g*a[3])*t1^4+1/3*(1/2*m*(6*(-a[2]*t1^2-a[3]*t1^3+x1)/t1*a[3]+4*a[2]^2)-m*g*a[2])*t1^3+1/2*(2*m*(-a[2]*t1^2-a[3]*t1^3+x1)/t1*a[2]-m*g*(-a[2]*t1^2-a[3]*t1^3+x1)/t1...](wirf2/wirf2_105.gif)
![9/10*m*a[3]^2*t1^5+1/4*(6*m*a[2]*a[3]-m*g*a[3])*t1^4+1/3*(1/2*m*(6*(-a[2]*t1^2-a[3]*t1^3+x1)/t1*a[3]+4*a[2]^2)-m*g*a[2])*t1^3+1/2*(2*m*(-a[2]*t1^2-a[3]*t1^3+x1)/t1*a[2]-m*g*(-a[2]*t1^2-a[3]*t1^3+x1)/t1...](wirf2/wirf2_106.gif)
| > |
Falls Sie mit Polynomen höheren Grades weiterarbeiten wollen, empfiehlt sich eine Vereinfachung des Terms.
| > | Ss:=simplify(S): |
| > |
Wir können nun die Wirkung als eine Funktion der Parameter (hier a2, a3) auffassen und die Variationsrechnung durch eine normale Extremwertsuche bei bekannter Funktion ersetzen, also das Minimum von S(a2,a3) bestimmen.
| > | sys:=seq(diff(Ss,a[j]),j=2..n); |
![sys := -1/60*m*(-30*a[3]*t1^5-20*t1^4*a[2]-10*t1^4*g)/t1, -1/60*m*(-48*a[3]*t1^6-30*t1^5*a[2]-15*t1^5*g)/t1](wirf2/wirf2_107.gif)
| > |
Die Lösung dieses Gleichungssystems muß exakt gelten, wir erwarten also a3=0 und a2=-1/2g
| > | #sol:=solve({sys},{a.(2..n)}); waere wegen Bereichsangabe elegant ... |
| > | sol:=solve({sys},{seq(a[i],i=1..n)}); |
![sol := {a[3] = 0, a[2] = -1/2*g, a[1] = a[1]}](wirf2/wirf2_108.gif)
| > |
Dies können wir in eine Weg-Zeit-Funktion xs einsetzen
| > | xs:=subs(sol,x(t)); |
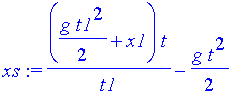
| > |
und zeichnen lassen, sobald die Konstanten festgelegt sind.
| > | m:=1: g:=10: t1:=2: x1:=3: xs;plot(xs,t=0..2); |
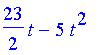
![[Maple Plot]](wirf2/wirf2_1011.gif)
| > |
Zum Vergleich die Lösung der Newtonschen Differentialgleichung:
| > | sol:=rhs(dsolve({diff(y(t),t$2)=-g,y(0)=0,y(t1)=x1},y(t))); |
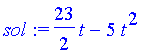
| > |
Nachdem wir uns versichert haben, daß das Ergebnis unserer Überlegungen der Newtonschen Physik nicht widerspricht, können wir uns wieder der ursprünglichen Absicht zuwenden, und die Wirkung längs gedachter Bahnen untersuchen, also die Ellipsengleichung in a2 und a3:
| > | a[2]:=a2: a[3]:=a3: |
| > |
(Diese Umsetzung von indizierten Variablen auf die Variablen a2, a3 ist für die folgenden Plotbefehle erforderlich: in den Bereichsangaben, können keine indizierten Variablen verwendet werden. Andererseits ist die Formulierung von Listen und deren Lösung mit solve (bzw. die Differentiation mit diff) mit indizierten Variablen einfacher.)
| > | Ss; |
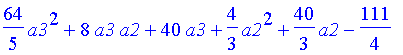
| > |
Im Parameterraum (a2,a3) werden die Linien gleicher Wirkung (Ss = const) also durch obigen Term beschrieben (Ellipsen). Was uns interessiert ist das Minimum der Wirkung also der Mittelpunkt dieser Ellipsen. Wir können es zunächst mit Schnitten längs der Parameterachsen versuchen:
| > | m:=1:t1:=2:x1:=3:a3:=0:a2:='a2': plot(Ss,a2=-10..0); |
![[Maple Plot]](wirf2/wirf2_1014.gif)
| > |
| > | m:=1:t1:=2:x1:=3:a3:='a3':a2:=-5: plot(Ss,a3=-1..1); |
![[Maple Plot]](wirf2/wirf2_1015.gif)
| > |
Den Überblick über eine Darstellung der Wirkung im Parameterraum bekommen wir aber am besten dreidimensional. Man muß allerdings in diesem Fall durch eine logarithmische Darstellung dem "schwachen Minimum" etwas auf die Beine helfen.
| > | a2:='a2': a3:='a3':t1:=1/2: |
| > | Ss; |
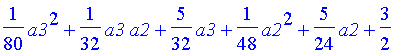
| > | plot3d(ln(Ss+80),a2=-8..-2,a3=-1..1,axes=boxed); |
![[Maple Plot]](wirf2/wirf2_1017.gif)
| > |
Auch hier finden wir eine Hilfe in dem Befehl <contourplot> (weitere Plots s.u. als Text) # in Maple V R5 schlechter...
| > | g:=10: t1:=2: |
| > | contourplot(ln(Ss+62),a2=-10..-1,a3=-2..2,axes=boxed,numpoints=2000,contours=20); |
![[Maple Plot]](wirf2/wirf2_1018.gif)
| > |
Die "falschen Bahnen" lassen sich also in Klassen einteilen, wenn man sie nach gleicher Wirkung sortiert. Dabei scheint die Natur in erster Linie darauf zu achten, daß der Bewegungs*typ* stimmt (steiler Anstieg der Wirkung in a3-Richtung), während sie es mit einer Abweichung in a2-Richtung nicht so genau nimmt. Besonders großzügig ist sie aber bei Abweichungen der Parameter in Richtung der Hauptachse, und besonders kleinlich in Richtung der Nebenachse. Wovon hängt die Orientierung der Achsen ab? Wie wirkt sich die Lage des Start- und Endpunktes aus? Was ändert sich mit g und m?
| > |
Vgl. Wheeler Gravitiation: "Die Natur hat es also so eingerichtet, daß bei linearem Potential nur a2 benötigt wird, und das mit passendem Wert". [jetzt käme die Physik, Kosmologie ... warum gerade so? Warum liegen die Ellipsen so? Warum die starke Änderung in die eine Richtung und die Unempfindlichkeit in die andere, bzw. was kann man daraus folgern? Diese weiterführenden und WESENTLICHEN Fragen liegen bei der Verwendung eines CAS eben viel näher und können leichter manipuliert werden.]
| > |
g:=1:t1:=1:
contourplot(Ss,a2=-10..10,a3=-2..2,axes=boxed,numpoints=2000,contours=20);
Oder eine etwas ausgefeiltere Darstellung der Linien gleicher Wirkung, die aber mehr Rechenzeit erfordert.
| > |
g:=10:t1:=2:a2:='a2':
implicitplot({seq(Ss=-60-0.1*i,i=1..10)},a2=-10..10,a3=-2..2,numpoints=5000,view=[-10..0,-2..2]);
m:='m':g:='g':t1:='t1':x1:='x1':
Ss;
| > |
komma@oe.uni-tuebingen.de