Moderne Physik mit Maple
PDF-Buch Moderne Physik mit Maple
Update auf Maple 10
Kapitel A.1
Worksheet madg1_10.mws
| > |
c ITP Bonn 1995 filename: madg1.ms
Autor: Komma Datum: 12.7.94
Thema: Behandlung gewöhnlicher Differentialgleichungen mit Maple
Gewöhnliche Differentialgleichungen
Vorweg ein paar technische Anmerkungen:
Packages und Rücksetzen von Variablen:
1.) Bei einmaligem Durchgang durch das Worksheet wäre die Wiederholung der with-Befehle überflüssig. In der Regel wird ein worksheet aber mehrmals und mit nicht voraussehbaren Sprüngen abgearbeitet. In diesem Fall können dann (etwa nach restart) die package-Befehle nicht mehr bekannt sein, bzw. Variable unzulässig belegt sein. Dagegen bieten die Wiederholungen der with-Befehle und unassignments eine gewisse Sicherheit.
Es taucht die Frage auf, ob das Package-Konzept nicht zu umständlich ist. Wünschenswert wäre eine kleine proc, die selbständig nach packages sucht.
2.) Die von Maple vergebenen Namen _C1, _C2 ... für Integrationskonstanten: die Nummer hängt von der Vorgeschichte ab. Das muß ggf. berücksichtigt werden, wenn in Befehlen auf diese Variablen Bezug genommen wird.
3.) Reihenfolge von Lösungen: ebenfalls nicht stabil, wenn Lösungs*mengen* berechnet werden. Insbes. ist der Bezug mit (") mit Vorsicht zu gebrauchen.
Schreibweise:
In diesem Abschnitt steht DG immer für gewöhnliche Differentialgleichung (eine unabhängige Variable).
Den Maple-Befehlen ist im Text ein "<" vorangestellt (... hoffentlich konsequent ...)
Eine DG der Ordnung r kann (explizit) so notiert werden:
y^(r)=f[x,y(x),y'(x),...,y^(r-1)]
Das ist eine Funktionalgleichung, in der neben der unabhängigen Variablen noch die gesuchte Funktion und ihre (r) Ableitungen vorkommen. In der Literatur zu DGn werden die Methoden zur Lösung nach steigendem Schwierigkeitsgrad geordnet behandelt. Das bedeutet in der Regel eine Einteilung in die zwei großen Abschnitte DG 1.Ordnung und DG höherer Ordnung, die dann weiter unterteilt werden in lineare und nicht-lineare Gleichungen, spezielle Typen von Gleichungen und Gleichungssysteme. Da wir mit unserem CAS ein elektronisches Handbuch zur Verfügung haben, müssen wir uns nicht so sehr um den Schwierigkeitsgrad oder gar die Theorie der Lösungsmethoden kümmern - das erledigt Maple für uns. Wir können vielmehr die für den Physiker und experimentellen Mathematiker interessanten Zusammenhänge in den Vordergrund stellen (soweit sie in diesem kurzen Anhang Platz haben) und uns im wahrsten Sinne des Wortes ein Bild davon machen, wie zum Beispiel der Typ der DG den Typ der Lösungsfunktion bestimmt (und umgekehrt). Deshalb beginnt dieser Abschnitt mit den mehr "handwerklichen" Aspekten, die zur Veranschaulichung der Lösungen einer DG dienen: Scharen von Lösungskurven, Richtungsfeld, Isoklinen, Trajektorien, Phasenportraits (man könnte noch ergänzen: Cauchy-Streckenzug und Picard-Lindelöf-Näherurng).
Wir beginnen mit der zentralen Fragestellung nach der Bestimmung und Darstellung von Lösungskurven:
Zur Lösung einer DG benötigt man zunächst nur den Befehl <dsolve(Gleichung, Funktion), wobei es zweckmäßig ist, die Gleichung nicht direkt in das Argument von <dsolve zu schreiben, sondern sie zu benennen.
| > | restart; |
| > | gl:=diff(y(x),x)=0; |
![]()
| > | dsolve(gl,y(x)); |
![]()
(Wir können ja auch mit Maple mit einer einfachen Gleichung beginnen.)
Oder etwas anspruchsvoller
| > | gl:=diff(y(x),x$3)=0; |
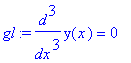
| > | dsolve(gl,y(x)); |
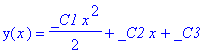
Jetzt haben wir schon drei Scharparameter, nämlich die drei Integrationskonstanten _C1, _C2 und _C3. Verwendet man die Option <laplace, so setzt Maple die Anfangsbedingungen in symbolischer Form ein. Dabei bedeutet z.B. D(y)(0) die erste Ableitung von y an der Stelle Null.
| > | dsolve(gl,y(x),method=laplace); |
![]()
Wir bleiben zunächst bei der Lösung mit den Integrationskonstanten und geben ihr einen Namen:
| > | sol:=rhs(dsolve(gl,y(x))); |
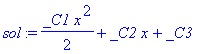
Eine Alternative wäre sol:=dsolve(gl,y(x));assign(sol);
Dann ist es aber nicht so einfach, die Lösung weiter zu bearbeiten.
Kurvenscharen werden in der Regel mit dem Befehl <seq dargestellt
| > | _C1:=1:_C2:=2:_C3:='_C3': |
| > | plot({seq(sol,_C3=-3..3)},x=-1..1,-2..2,scaling=constrained); |
![[Maple Plot]](madg1/madg1_107.gif)
Mit kleinerer Schrittweite:
| > | plot({seq(sol,_C3=seq(-3+0.5*i,i=0..15))},x=-1..1,-2..2,scaling=constrained); |
![[Maple Plot]](madg1/madg1_108.gif)
Abb.
read `fig.m`:pspl(`p1madg1.ps`):
vtitle:=``:vxlab:=`x`:vylab:=`y`:
plot({seq(sol,_C3=seq(-3+0.5*i,i=0..15))},x=-1..1,-2..2,scaling=constrained,opt2d); winpl();
Oder dreidimensional:
| > | _C3:='_C3': |
| > | plot3d(sol,_C3=-3..3,x=-1..1,view=-3..4,style=wireframe,orientation=[-140,80],axes=frame); |
![[Maple Plot]](madg1/madg1_109.gif)
| > |
Jetzt können Sie im Prinzip schon jede DG lösen, die Maple lösen kann, und sich ein Bild von der Lösung machen. Wie wäre es mit folgender Fragestellung: "Wie sieht die Lösung einer DG 1.Ordnung aus, in der ein Polynom in y vorkommt?"
Das Primitivpolynom y(x)=0 hatten wir schon oben. Der nächste Schwierigkeitsgrad wäre dann y(x):
| > | gl:=diff(y(x),x)=y(x);dsolve(gl,y(x)); |
![]()
![]()
Diese wohlbekannte Lösung erscheint in neuem Licht, wenn wir zu y(x)^n fortschreiten:
| > | gl:=diff(y(x),x)=y(x)^n;dsolve(gl,y(x)); |
![]()
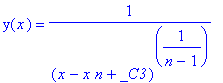
Bei einem "echten Polynom" wird es noch schwieriger
| > | gl:=diff(y(x),x)=a*y(x)^3+b*y(x)^2+c*y(x); |
![]()
| > | dsolve(gl,y(x)); |
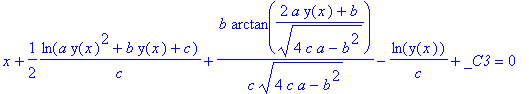
Und bei gebrochen rat. Fktn. in y? (rechnen Sie mit einer längeren Ausgabe!)
| > | gl:=diff(y(x),x)=a*y(x)^3+b*y(x)^2+c/y(x); |
![]()
| > | dsolve(gl,y(x),explicit); |
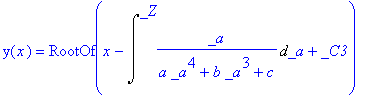
läuft in R3
| > |
| > |
Nach diesem ersten Ausflug in das abwechslungsreiche Land der Differentialgleichungen können wir unsere mathematischen Experimente zum Zusammenhang DG <--> Integralkurven mit der Frage nach der Eindeutigkeit des Kurventyps fortsetzen. Man kann sich z.B. vorstellen, daß man experimentell einen funktionalen Zusammenhang zwischen zwei Größen bestimmt hat, und nun die Bewegungsgleichung (im verallgemeinerten Sinn) sucht. Mit dieser Fragestellung können wir gleichzeitig testen, welche Lösungsmethoden Maple einsetzt. Wir wählen uns die leicht überschaubare Funktion y=x^2 (als experimentell gefundenes "Gesetz") und konstruieren dazu fünf DGn.
| > | dg1:=y(x)+diff(y(x),x)=x^2+2*x; |
![]()
| > | dg2:=y(x)*diff(y(x),x)=2*x^3; |
![]()
| > | dg3:=y(x)/diff(y(x),x)=x/2; |
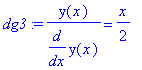
| > | dg4:=diff(y(x),x)/y(x)=2/x; |
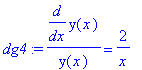
| > | dg5:=y(x)=diff(y(x),x)^2/4; |
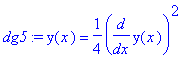
Und lassen lösen:
| > | for i to 5 do dsolve(dg||i, y(x)) od; |
![]()
![]()
![]()
![]()
![]()
[Vor Maple 6: Nur mit der vierten DG erhalten wir wieder den einfachen angesetzten Funktionstyp, weil in dieser Gleichung die Variablen schon getrennt sind. Die zweite, dritte und fünfte Gleichung führen zu implizit gegebenen Lösungen, die sich aber mit der Option <explicit im Argument von <dsolve vermeiden lassen, z.B.:
dsolve(dg2,y(x),explicit);
(bei der dritten Gleichung kommen dann zwei konjugiert komplexe Lösungen hinzu). ]
So weit die ersten Befehle zur Lösung. Wie sieht die Lösung aus?
Ein wichtiges Hilfsmittel zur Veranschaulichung der Lösungsmenge einer DG ist das Richtungsfeld (also y' als Funktion von x und y), das man im Falle der DG 1.Ordnung einfach durch Auflösen der DG nach y' erhält. Maple hat dafür den Befehl <dfieldplot im package DEtools. Wir können uns die fünf Richtungsfelder zusammen mit der einfachsten Lösung zeigen lassen.
[Bitte warten Sie, bis *fünf* Plots erschienen sind ...]
In Maple 6 nur vier, der fünfte bringt eine Fehlermeldung
| > | with(DEtools): with(plots): |
| > | for i to 5 do |
| > | display({plot(x^2,x=-2..2),dfieldplot(dg||i,y(x),x=-2..2,y=-2..2,scaling=constrained)}) od; |
![[Maple Plot]](madg1/madg1_1028.gif)
![[Maple Plot]](madg1/madg1_1029.gif)
![[Maple Plot]](madg1/madg1_1030.gif)
![[Maple Plot]](madg1/madg1_1031.gif)
Plotting error, non-numeric vertex definition
| > |
Nicht mehr gültig in Maple 6
Zu einer Funktion haben wir also fünf DGn und zu vier dieser DGn haben wir jeweils eine weitere Lösung bekommen. Das bedeutet aber umgekehrt auch, daß man sich sorgfältig überlegen muß, in welcher Form man Maple eine DG vorlegt, denn man bekommt in (diesen) vier von fünf Fällen nicht die einfachste Lösung. Man muß aber auch darauf gefaßt sein, daß das Richtungsfeld nicht zur vorgeschlagenen Lösung paßt. Vielleicht haben Sie es schon bemerkt ... die explizite Lösung von dg3 lautet:
| > | dsolve(dg3,y(x),explicit); |
![]()
Also sehen die reellen Integralkurven zu dg3 so aus:
| > | plot({seq((c*x)^(2/3),c=-5..5)},x=-2..2); |
![[Maple Plot]](madg1/madg1_1033.gif)
Und das sind Kurven, die nur im singulären Punkt (0|0) zu den anderen Lösungen passen, es empfiehlt sich also, die Probe zu machen:
Das kann man natürlich auch selbst machen:
| > | for i to 4 do ys||i:=subs(y(x)=y,solve(dg||i,diff(y(x),x))) od; ys5:=subs(y(x)=y,{solve(dg5,diff(y(x),x))}); |
![]()
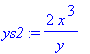
![]()
![]()
![]()
Neben dem Richtungsfeld gibt es noch ein zweites Hilfsmittel zur Untersuchung der Lösungsfunktionen von DGn:
Es gibt mit Maple einen einfachen Trick, sich ohne viel Mathematik ein Bild von den Kurven gleicher Steigung zu verschaffen. Man stellt die Steigung (y') als Funktion von x und y dreidimensional dar (zu diesem Zweck wurde oben y(x) durch y substituiert, weil y(x) nicht in der Bereichsangabe akzeptiert wird). Diese Darstellung bekommt noch mehr Aussagekraft, wenn man im Plot die Option style=contour wählt und den Plot von oben betrachtet:
| > | plot3d(ys3,x=-2..2,y=-2..2,view=-4..4); |
![[Maple Plot]](madg1/madg1_1039.gif)
Als es noch keine CASe gab, mußte man die Isoklinen von Hand zeichnen und sie dann "mit Linienelementen bespicken". Mit Maple benötigen wir dazu nur zwei Befehle (es wäre zu aufwendig, an dieser Stelle die Linienelemente genau auf die Isoklinen zu setzen, deshalb begnügen wir uns mit der zweidimensionalen Darstellung der Isoklinen zusammen mit dem Richtungsfeld):
| > | iso:=solve(ys1=a,y); |
![]()
| > | display({plot({seq(iso,a=-3..3)},x=-2..2),dfieldplot(dg1,y(x),x=-2..2,y=-2..2,scaling=constrained)}); |
![[Maple Plot]](madg1/madg1_1041.gif)
Abb.
pspl(`p9madg1.ps`):
display({plot({seq(iso,a=-3..3)},x=-2..2),dfieldplot(dg1,y(x),-2..2,-2..2,scaling=constrained)},opt2d);winpl():
Das dritte Hilsmittel bei der Untersuchung von DGn sind die
In der Physik benötigt man oft die Gleichung und Darstellung einer Kurvenschar, deren Kurven mit den Kurven einer gegebenen Schar einen bestimmten Winkel bilden (Feld -- Potential, Wellenfront -- Strahl, ...). Diese Aufgabe läßt sich leicht bewerkstelligen, wenn man die DG (1.Ordnung) der gegebenen Schar hat. Zu der Schar mit y'=f(x) lautet die DG der Trajektorien: yt'=(1+cf)/(c-f) , mit c als Cotangens des eingeschlossenen Winkels.
| > | f:='f': c:='c': |
| > | dg:=diff(y(x),x)=f; |
![]()
| > | dgt:=diff(y(x),x)=(1+c*f)/(c-f); |
![]()
Wählen wir als einfaches Beispiel für Trajektorien (oder Äquipotentiallinien - bei umgekehrter Problemstellung) Strahlen, d.h. Ursprungsgeraden
| > | f:=y(x)/x; |
![]()
so erhalten wir die Gleichung der logarithmischen Spirale in etwas ungewohnter Form
| > | dsolve(dgt,y(x)); |
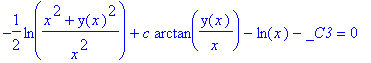
Das Richtungsfeld kann ohne weiteres gezeichnet werden
| > | with(DEtools): |
| > | c:=0.1: |
| > | p1:=dfieldplot(dgt,y(x),x=-2..2,y=-2..2,scaling=constrained): |
| > | p1; |
![[Maple Plot]](madg1/madg1_1046.gif)
Für eine Scharkurve schreiben wir die logarithmische Spirale in Parameterform
| > | c:=0.1: R:=0.2: |
| > | r:=R*exp(c*t); |
![]()
| > | p2:=plot([r*cos(t),r*sin(t),t=0..20]):p2; |
![[Maple Plot]](madg1/madg1_1048.gif)
| > | with(plots): |
| > | display({p1,p2}); |
![[Maple Plot]](madg1/madg1_1049.gif)
Abb.
pspl(`p10madg1.ps`):
display({p1,p2},opt2d);winpl():
(Aufgabe: ergänzen Sie den vorangehenden Plot durch die Darstellung der Strahlen ... zwei davon werden automatisch dargestellt)
Eine interessantere Aufgabe:
Bestimmung der Orthogonaltrajektorien zu einer Schar ähnlicher Ellipsen mit gleichem Mittelpunkt.
DGn der Kurvenscharen:
| > | restart; with(DEtools):with(plots): |
| > | dg:=diff(y(x),x)=f: |
| > | dgt:=diff(y(x),x)=(1+c*f)/(c-f): |
Ellipsengleichungen (z.B. Verhältnis der Halbachsen n=a/b, denn wir benötigen ja nur *einen* Scharparameter)
| > | el:=x^2/a^2+y(x)^2/b^2=1; b:=a/n; |
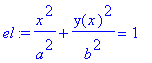
![]()
Elimination des Scharparameters
| > | asol:=solve(el,a); |
![]()
DG der Ellipsenschar
| > | dgl:=subs(a=asol[1],diff(el,x)); |
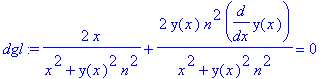
Also ist die rechte Seite der DG 1.Ordng.
| > | f:=solve(dgl,diff(y(x),x)); |
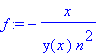
Probe (bei Wiederholung mit anderem n hier wieder einsteigen)
| > | n:=sqrt(3): |
| > | probe:=dsolve(dg,y(x),explicit); |
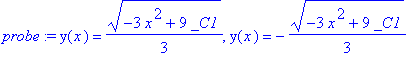
Eine ganze Ellipse als Liste zweier halber Ellipsen:
| > | sol:=rhs(probe[1]),rhs(probe[2]): |
Schau' mer mal, wie's ausschaut:
| > | pel:=plot({seq(sol,_C1=seq(0.2*i,i=1..5))},x=-2..2,color=blue,scaling=constrained): |
| > | pel; |
![[Maple Plot]](madg1/madg1_1056.gif)
Aber nun kommt die eigentliche Arbeit, also die Bestimmung der Orthogonaltrajektorien
| > | c:=0: |
| > | solt:=rhs(dsolve(dgt,y(x),explicit)); |
![]()
Das sind also ganz normale Potenzfunktionen ...
| > | ptra:=plot({seq(solt,_C1=seq(0.2*i,i=-5..5))},x=-2..2,color=black,scaling=constrained): |
| > | ptra; |
![[Maple Plot]](madg1/madg1_1058.gif)
Und stehen die auch wirklich (senkrecht) auf den Ellipsen?
| > | with(plots): with(DEtools): |
| > | display({dfieldplot(dgt,y(x),x=-2..2,y=-2..2),dfieldplot(dg,y(x),x=-2..2,y=-2..2),pel,ptra}); |
![[Maple Plot]](madg1/madg1_1059.gif)
| > |
Abb.
read `fig.m`:vtitle:=``:vxlab:=``:vylab:=``:pspl(`p11madg1.ps`):
display({dfieldplot(dgt,y(x),-2..2,-2..2),dfieldplot(dg,y(x),-2..2,-2..2),pel,ptra},opt2d);winpl():
Sie können nun oben ein anderes n einsetzen und so Ellipsenscharen verschiedener Exzentrizität erzeugen (bitte dabei auf die Numerierung der _C's achten)
... und für die Spezialisten:
Was ergibt sich für imaginäres n?
Aber Spezialisten wissen das natürlich! Doch hatten sie (die Spezialisten) schon jemals ein Werkzeug, mit dem man das so mühelos zeigen konnte?
=====================================
Weitere Beispiele:
DG vom Riccati-Typ (dg ist weiterhin y'=f):
| > | f:=x^2+y(x)^2; z:=rhs(dsolve(dg,y(x))); |
![]()

Maple weiß uns also auch hier zu helfen, wenn wir etwas Geduld aufbringen und den Namen der Integrationskonstanten richtig wählen (im Beispiel _C1, das kann sich aber von session zu session ändern).
| > | _C1:=1: |
| > | plot(z,x=-3..3,-3..3); |
![[Maple Plot]](madg1/madg1_1062.gif)
Richtungsfeld und Isoklinen
| > | display({dfieldplot(dg,y(x),x=-2..2,y=-2..2,scaling=constrained),seq(polarplot(r),r=1..2)}); |
![[Maple Plot]](madg1/madg1_1063.gif)
Im letzten Befehl wurden die kreisförmigen Isolklinen mit <polarplot gezeichnet. Die allgemeinere Version ist
| > | ipl:=implicitplot({seq(subs(y(x)=yy,f)=const,const=1..2)},x=-2..2,yy=-2..2): ipl; |
![[Maple Plot]](madg1/madg1_1064.gif)
| > | display({dfieldplot(dg,y(x),x=-2..2,y=-2..2,scaling=constrained),ipl}); |
![[Maple Plot]](madg1/madg1_1065.gif)
Nun können Sie ein anderes f eingeben und die Richtungsfelder und Isoklinen IHRER Funktionen untersuchen.
Wir verwenden das letzte Beispiel, zu einer weiteren Demonstration der DEtools, nämlich der
Phasenportraits (hier als Näherungsmethode eingesetzt):
Integralkurven einer expliziten DG 1. Ordnung können auch mit dem Befehl <phaseportrait (in DEtools) dargestellt werden. Die zur Verfügung stehenden Integrationsmethoden sind in DEtools[options] beschrieben (Euler-Cauchy-Streckenzug, Runge-Kutta, ...):
| > | f:=y(x)^2+x^2; |
![]()
| > | phaseportrait(dg,[y(x)],-1..1,{[1,0],[1,.2],[1,.4],[1,.7],[1,1.2]}); |
![[Maple Plot]](madg1/madg1_1067.gif)
| > |
| > | #display({%,dfieldplot(dg,y(x),x=-2..2,y=-2..2)}); |
Mit dieser Methode bekommt man allerdings bei singulären Punkten Schwierigkeiten, z.B. bei folgender Funktion:
| > | f:=2*y(x)/x: phaseportrait(dg,[y(x)],-1..1,{[1,0],[1,.2],[1,.4],[1,.7],[1,1.2]}); |
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
![[Maple Plot]](madg1/madg1_1068.gif)
Noch ein Hinweis zur Verwendung von <phaseportrait:
Bei zu großer Schrittweite erzeugt Maple in der Nähe von Singularitäten "moderne Kunst"
| > | f:=x/y(x): phaseportrait(dg,[y(x)],-1..1,{[1,.1],[1,.2],[1,.4],[1,.7],[1,1.2]}); |
![[Maple Plot]](madg1/madg1_1069.gif)
Das läßt sich auch mit der Option <stepsize nicht immer beheben.
| > | phaseportrait(dg,[y(x)],-1..1,{[1,.1],[1,.2],[1,.4],[1,.7],[1,1.2]},stepsize=0.02); |
Warning, plot may be incomplete, the following errors(s) were issued:
division by zero
![[Maple Plot]](madg1/madg1_1070.gif)
Dabei haben wir doch eine so einfache Lösung ...
| > | dsolve(dg,y(x),explicit); |
![]()
| > |
| > |
komma@oe.uni-tuebingen.de